正弦定理 ：
　　　　　

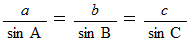
（ 証 明 ）
　　　　　

　　　　　



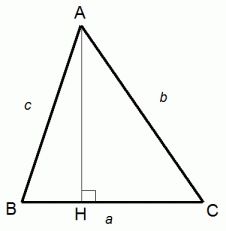
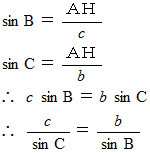
　 どんな三角形でも外接円を描くことができます。 外接円の中心は、 三角形の２辺のそれぞれの垂直二等分線の交点になります。 外接円の半径の長さを R とすると、 次の式が成り立ちます。
　　　　　

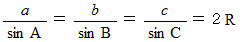
（ 証 明 ）
　　　　　

　　　　　円周角の定理より、
　　　　　　　　　
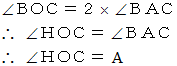
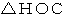　　　　　 は直角三角形だから、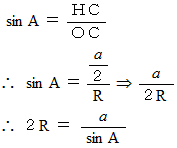
　　　　　　　　　



命題 ：　三角形の一辺が外接円の直径の長さに等しいならば、 その三角形は直角三角形である。

（ 証 明 その１ ）
　　　　　

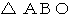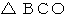　　　　　と　 は２等辺三角形である。
　　　　三角形の内角の和は π だから、
　　　　　　　　
　　　　　　　　
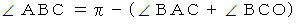
　　　　したがって、
　　　　　　　　
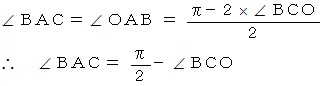
　　　　よって、
　　　　　　　　


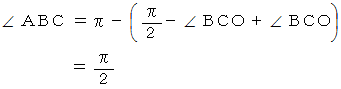
（ 証 明 その２ ）
　　　　円周角の定理より、
　　　　　　　　
　　　　


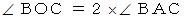
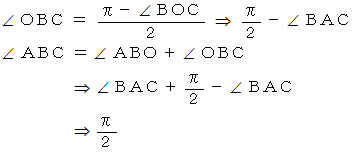
円周角の定理 ：
　　　　１つの弧に対する円周角の大きさは一定であり、 その弧に対する中心角の半分である。
　　　その証明については、 多治見中学学習ページ が解りやすいと思います。
　　　http://dac.gijodai.ac.jp/it-con/h16_sakuhin/ippan/ippan3/math/3grade/circle/circle5.htm