【 問 題 】

　正五角形ＡＢＣＤＥの頂点Ａから重心Ｏを貫いて対辺ＣＤの中点Ｍに至る線分ＡＭ と 対辺ＣＤに平行な対角線ＢＥ との交点をＰとする。ＯＡの長さは 1 である。

　　　　

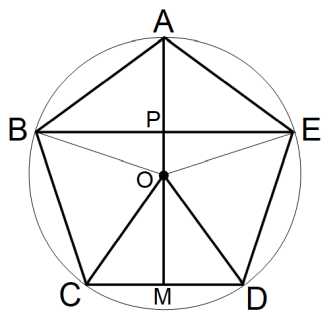
（１） ＣＤ および ＢＥ の長さを求めよ。
（２） ＣＤの長さに対するＢＥの長さの比が黄金比であることを示せ。
（３） ＯＡの長さ に ＯＰの長さの２倍 を加えたものは、ＯＭの長さの２倍に等しいことを示せ。
（４） （３）を ベクトル解析を用いて簡単に証明せよ。

【 解 答 】

（１）

ＡＢ ＝ ＢＣ ＝ ＣＤ ＝ ＤＥ ＝ ＥＡ
ＯＡ ＝ ＯＢ ＝ ＯＣ ＝ ＯＤ ＝ ＯＥ ＝ 1
∠ＡＯＢ ＝ ∠ＢＯＣ ＝ ∠ＣＯＤ ＝ ∠ＤＯＥ ＝ ∠ＥＯＡ ＝ 72°

まず、 cos 72° を求める。次の図を利用する。（ △ＡＣＤと相似な図形である。 ）
　　　

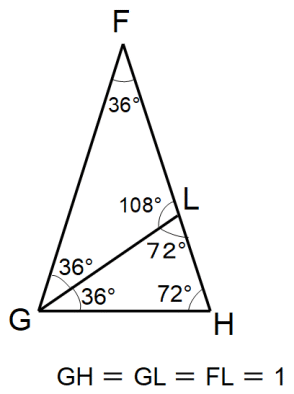
ＦＧの長さを x とする。
△ＦＧＨ と △ＧＨＬ は相似だから、
ＦＧ：ＧＨ ＝ ＧＨ：ＨＬ
よって、 ＦＧ × ＨＬ ＝ ＧＨ²
よって、 ＦＧ × (ＦＨ−ＦＬ) ＝ ＧＨ²
よって、 ＦＧ × (ＦＧ−ＧＨ) ＝ ＧＨ²
よって、 x × ( x − 1 ) ＝ 1²
よって、 x² − x − 1 ＝ 0
解の公式より、
　　　
△ＦＧＨ における余弦定理より、
　　　


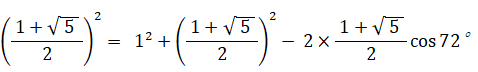
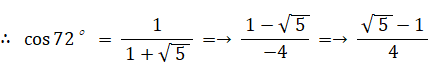
次に、 sin 72° を求める。
　　　
　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　

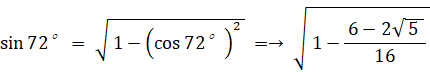
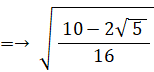
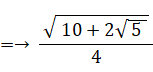
△ОＣＤにおける余弦定理より、ＣＤの長さは次のようになる。
　　　
　　　　　　　　　　　　
　　　　　　　　　　　　
　　　　　　　　　　　　
　　　　　　　　　　　　

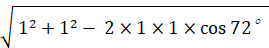
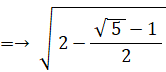
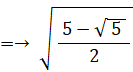
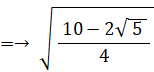
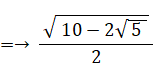
ＢＥ ＝ 2×ＢＰ ＝→　2 × ( 1×sin 72° )
　　　　　　　　

（２）

　　　　　　　　　　　　　
　　　　　　　　　　　　　
　　　　　　　　　　　　　
　　　　　　　　　　　　　

（３）

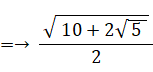
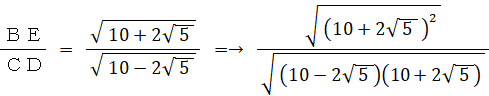
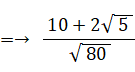
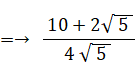
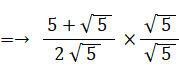
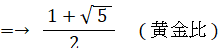
ＯＰ ＝ 1×cos 72°
　　

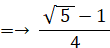
△ОＣМにおいてピタゴラスの定理より、ОМの長さは次のようになる。
　　　
　　　　　　　　　
　　　　　　　　　
　　　　　　　　　




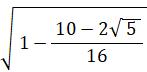
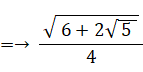
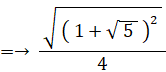
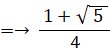
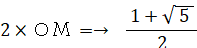
というわけで、ＯＡの長さ に ＯＰの長さの２倍 を加えたものは、ＯＭの長さの２倍に等しいことが分かった。

（４）

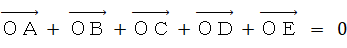　より、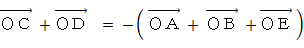
　　　
　　　
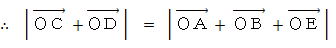
ところで、
　　　
　　　
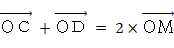
したがって、
　　　
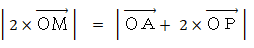
というわけで、（３）が簡単に証明された。