正三角形の対称群は自転と鏡映で構成されます。
　　　　　　

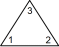
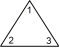
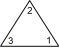
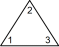
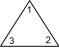
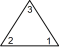
　型紙を切り抜いて正三角形を作ります。それを底辺がどれか分かりやすいようにして机の上に置きます。底辺の左側の角に 1 と記入し、底辺の右側の角に 2 と記入し、頂角に 3 と記入します。次に正三角形を裏返し、３つの角に表と同じ数を記入します。正三角形の表裏の区別はしないものとします。上図の一番左側の正三角形の姿勢を ( 1 2 3 ) と表し、一番右側の正三角形の姿勢を ( 2 1 3 ) と表すことにします。

　自転（ ０度以上 360 度未満 ）で姿勢が変わっても変換前と格好が全く同じになるとき、点対称 といいます。また、鏡映 で姿勢が変わっても変換前と格好が全く同じになるとき、線対称 といいます。
　点対称または線対称を担う演算子を対称群の元とします。元は全部で６個あります。
　例えば、< 1 2 3 >( 2 3 1 ) は、( 2 3 1 ) の姿勢になっている正三角形を時計回りに 120 度自転させる演算を表します。
　　　　　　　　　　　　　※ 参考： 大学生のための数学 ＞ 論理学 ＞ 群とは

　たとえば、( 1 3 2 ) の姿勢の三角形に対して演算を行います。

　　１　時計回りに ０度自転 ：
　　　　　　<　>( 1 3 2 ) ＝→ ( 1 3 2 )
　　２　時計回りに 120 度自転 ：
　　　　　　< 1 2 3 >( 1 3 2 ) ＝→ ( 3 2 1 )
　　　　　　　　　※　１番目の場所にある数は２番目の場所にある数に置き換えられ、
　　　　　　　　　　　２番目の場所にある数は３番目の場所にある数に置き換えられ、
　　　　　　　　　　　３番目の場所にある数は１番目の場所にある数に置き換えられる。
　　３　時計回りに 240 度自転 ：
　　　　　　< 1 3 2 >( 1 3 2 ) ＝→ ( 2 1 3 )
　　４　重心と底辺の右側の角を結ぶ直線に対する鏡映 ：
　　　　　　< 2 3 >( 1 3 2 ) ＝→ ( 1 2 3 )
　　５　重心と底辺の左側の角を結ぶ直線に対する鏡映 ：
　　　　　　< 1 3 >( 1 3 2 ) ＝→ ( 2 3 1 )
　　　　　　　　　※　１番目の場所に存在する数は３番目の場所に存在する数に置き換えられ、
　　　　　　　　　　　３番目の場所にある数は１番目の場所にある数に置き換えられる。
　　　　　　　　　※　置換群のように、
　　　　　　　　　　　１という数は３という数に置き換えられ、
　　　　　　　　　　　３という数は１という数に置き換えられる、のではありません。
　　　　　　　　　※　置換群のように、
　　　　　　　　　　　１がある場所は、１を捨てて３を得て、
　　　　　　　　　　　３がある場所は、３を捨てて１を得る、のではありません。
　　　　　　　　　　　　　参照： 大学生のための数学 ＞ その他の数学 ＞ 置換群（ 対称群 ）
　　６　重心と頂角を結ぶ直線に対する鏡映 ：
　　　　　　< 1 2 >( 1 3 2 ) ＝→ ( 3 1 2 )

　例えば、２をしてから６をすることを < 1 2 >< 1 2 3 > と表すことにします。これは < 1 3 > という変換と等しいです。


群の乗積表 ：　＊ 第１行の第２列〜第７列は かけられる元、 第２行〜第７行の第１列は かける元

	１	２	３	４	５	６
１	１	２	３	４	５	６
２	２	３	１	５	６	４
３	３	１	２	６	４	５
４	４	６	５	１	３	２
５	５	４	６	２	１	３
６	６	５	４	３	２	１


　　１ ：　<　>　　　　２ ：　< 1 2 3 >　　　３ ：　< 1 3 2 >
　　４ ：　< 2 3 >　　　５ ：　< 1 3 >　　　　６ ：　< 1 2 >