【 問 題 】

x y − ３x − ４y ＋ 11 ＝ ０　を満たす 整数 x と y のペアを求めよ

【 解 答 】

問題の式が成り立つための必要十分条件は、 次の式が成り立つことである。
　　x y − ３x − ４y ＋ 12 ＝ １
上の式が成り立つための必要十分条件は、 次の式が成り立つことである。
　　( x − ４ ) ( y − ３ ) ＝ １
上の式が成り立つための必要十分条件は、 次のとおりである。
　　（　x−４ ＝ １　かつ　y−３ ＝ １　） または （　x−４ ＝ −１　かつ　y−３ ＝ −１　）
したがって、 答えは次の２組である。
　　（ x, y ）＝（ ５, ４ ）　と　（ x, y ）＝（ ３, ２ ）

【 別 解 】

問題の式が成り立つための必要十分条件は、 次の式が成り立つことである。
　　（ x − ４ ）y　＝　３x − 11
上の式は x＝４ のとき成り立たない。
したがって、 上の式が成り立つための必要十分条件は、 次の式が成り立つことである。
　　
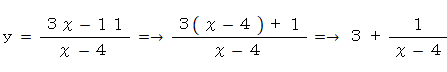
y は整数なので、上の式が成り立つための必要十分条件は、 次のとおりである。
　　x ＝ ５　または　x ＝ ３
したがって、 答えは次の２組である。
　　（ x, y ）＝（ ５, ４ ）　と　（ x, y ）＝（ ３, ２ ）