その他の数学 へ戻るくじのＡを選んだ人を
さん 、 Ｂを選んだ人を 
さん、 Ｃを選んだ人を 
さん、・ ・ ・ ・ というふうにします。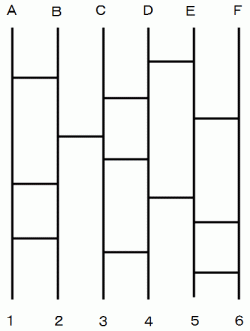
あみだくじは 置換 です。 このあみだくじの置換は次のように表されます。
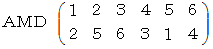
しかし、 よく次のように間違えらます。
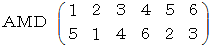
置換とは、 置く場所の入れ替えです。 それぞれの場所は固定されていて、 数字だけが動きます。 したがって、 置換とは数列の変換になります。 一方、後者は大きさの等しい集団どうしの全単射による数の変換です。 このように、 置換はよく誤解されますので、 間違いが生じないようにするため、 次のようにすることを提案させていただきます。
本当の置換とは「 置換演算子 」が関与する数を置き換えるという演算のことである。
演算が行われた後に、同じ位置にある変換前の数から変換後の数への写像としてみる見方を「 全単射数変換演算子 」が関与する「 全単射数変換写像 」 とする。
演算が行われた後に、同じ位置にある変換前の数から変換後の数への写像としてみる見方を「 全単射数変換演算子 」が関与する「 全単射数変換写像 」 とする。
（１） 本当の置換
-
６つの１〜６の自然数が小さい順に並んだ順列
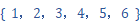があります。巡回置換演算子 [1,3,5,2,6] は、 次の６つの操作を同時に一瞬にする演算子です。
-
1 のある場所は 1 を捨てて 3 を獲得し、
3 のある場所は 3 を捨てて 5 を獲得し、
5 のある場所は 5 を捨てて 2 を獲得し、
2 のある場所は 2 を捨てて 6 を獲得し、
6 のある場所は 6 を捨てて 1 を獲得し、
4 のある場所は 4 をキープする。
「 巡回置換 」のうち２つの数のみ置換するものを「 互換 」と言います。
「 巡回置換 」は「 互換 」の合成で表すことができる。
( 3 6 5 4 2 1 ) ＝ [1,3,5,2,6]( 1 2 3 4 5 6 )
＝→ [1,5,2,6][1,3]( 1 2 3 4 5 6 ) ＝→ [1,5,2,6]( 3 2 1 4 5 6 )
＝→ [1,2,6][1,5][1,3]( 1 2 3 4 5 6 ) ＝→ [1,2,6][1,5]( 3 2 1 4 5 6 ) ＝→ [1,2,6]( 3 2 5 4 1 6 )
＝→ [1,6][1,2][1,5][1,3]( 1 2 3 4 5 6 ) ＝→ [1,6][1,2]( 3 2 5 4 1 6 ) ＝→ [1,6]( 3 1 5 4 2 6 )
＝→ ( 3 6 5 4 2 1 )
-
６つの１〜６の自然数が小さい順に並んだ順列
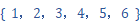があります。全単射数変換演算子
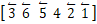は、 次の６つの操作を同時に一瞬にする演算子です。-
数 1 を 数 3 に変換する。
数 2 を 数 6 に変換する。
数 3 を 数 5 に変換する。
数 4 はそのままにする。
数 5 を 数 2 に変換する。
数 6 を 数 1 に変換する。
ある「 全単射数変換 」 は 他の「 全単射数変換 」 の合成で表すことができる。
