乮侾乯懳捀妏偼摍偟偄
-
佢俙俤俠 亖 佢俢俤俛丂偺徹柧
丂丂丂
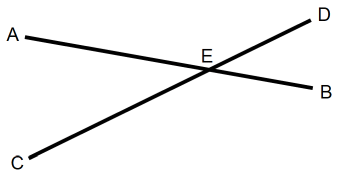
丂丂丂佢俙俤俠 亄 佢俙俤俢 亖 180亱
丂丂丂佢俢俤俛 亄 佢俙俤俢 亖 180亱
丂傛偭偰丄
丂丂丂佢俙俤俠 亄 佢俙俤俢 亖 佢俢俤俛 亄 佢俙俤俢
丂傛偭偰丄
丂丂丂佢俙俤俠 亖 佢俢俤俛
-
仩俙俛俠俢 偺撪妏偺榓偑360亱偱偁傞偙偲偺徹柧
丂丂丂
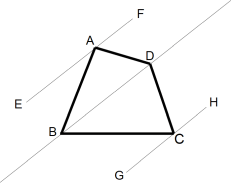
丂丂丂丂丂丂丂丂丂丂俛俢 // 俤俥 // 俧俫
丂丂丂佢俙俛俢 亖 佢俛俙俤
丂丂丂佢俙俢俛 亖 佢俢俙俥
丂傛偭偰丄
丂丂丂佢俛俙俢 亄 佢俙俛俢 亄 佢俙俢俛 亖 180亱
丂丂丂佢俠俛俢 亖 佢俛俠俧
丂丂丂佢俠俢俛 亖 佢俢俠俫
丂傛偭偰丄
丂丂丂佢俛俠俢 亄 佢俠俛俢 亄 佢俠俢俛 亖 180亱
丂偟偨偑偭偰丄
丂丂丂仩俙俛俠俢 偺撪妏偺榓
丂丂丂丂丂丂丂亖 佢俛俙俢 亄 ( 佢俙俛俢 亄 佢俠俛俢 ) 亄 佢俛俠俢 亄 ( 佢俙俢俛 佢俠俢俛)
丂丂丂丂丂丂丂亖仺丂( 佢俛俙俢 亄 佢俙俛俢 亄 佢俙俢俛 ) 亄 ( 佢俛俠俢 亄 佢俠俛俢 亄 佢俠俢俛 )
丂丂丂丂丂丂丂亖仺丂180亱 亄 180亱 亖仺丂360亱
-
佢俫俤俛 亖 佢俤俥俻 偺徹柧
丂丂丂
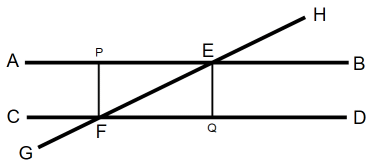
丂丂丂丂丂丂丂俙俛 // 俠俢
丂丂丂丂丂丂丂俙俛偵悅捈側曗彆慄暘俹俥傪堷偔丅
丂丂丂丂丂丂丂俠俢偵悅捈側曗彆慄暘俤俻傪堷偔丅
丂嶰妏宍偺撪妏偺榓偼180亱偩偐傜丄
丂丂丂俹俥偼俠俢偵悅捈偱偁傞丅 丒丒丒 嘆
丂丂丂俤俻偼俙俛偵悅捈偱偁傞丅
丂偟偨偑偭偰丄
丂丂丂仩俹俥俻俤偼挿曽宍偱偁傞丅
丂傛偭偰丄
丂丂丂仮俹俥俤 偲 仮俻俤俥 偼崌摨偱偁傞丅
丂偟偨偑偭偰丄
丂丂丂佢俤俥俻 亖 佢俥俤俹
丂懳捀妏偼摍偟偄偺偱丄
丂丂丂佢俫俤俛 亖 佢俥俤俹
丂傛偭偰丄
丂丂丂佢俫俤俛 亖 佢俤俥俻
-
乮俀乯偲乮俁乯偺徹柧偼丄寋偑愭偐棏偑愭偐偺娭學偵側偭偰偄傑偡丅
偦偙偱丄乮俁乯偺 嘆 偼徹柧偡傞偙偲偺偱偒側偄丄岞弨偱偁傞偲尒側偝傟偰偄傑偡丅
嫽枴偺偁傞曽偼乽暯峴慄岞弨栤戣乿偵偮偄偰挷傋偰傒偰偔偩偝偄丅
 婔壗妛 傊栠傞
婔壗妛 傊栠傞