【 問 題 】

３辺の長さが　ルート３　と　ルート３　と　２　の二等辺三角形が４つ、 一辺の長さが ２ の正方形が １つあります。
これら５つの平面を使ってピラミッド型の角錐 （ 四角錐 ） を作ります。
この角錐の体積を 四角錐の体積の公式 や 積分 を使わないで求めてください。

【 解 答 】

　　　　　　　

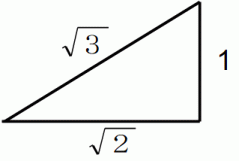
正方形の重心と頂点を結ぶ線分の長さは　ルート２　です。
したがって、 四角錐の高さは　ルート｛（ルート３）² −（ルート２）² ｝ ＝→　１　になります。
この四角錐を２つ持ってきて、 頂点どうしを接触させて底面どうしを平行にします。
次に、 この四角錐を４つ持ってきて４方向から頂点を一点に重ねるように組み込みます。
すると、 縦 横 高さ がそれぞれ２の立方体になります。
この立方体の体積は ２³　＝→　８　です。
したがって、 四角錐の体積は　8/6　＝→　4/3　です。

【 備 考 】

四角錐の底面の面積は ４ で、 四角錐の高さは １ です。
したがって、 角錐の体積の公式より、 この四角錐の体積は次のようになります。
　　　　 1/3　× ４ × １　＝→　4/3

積分によってこの四角錐の体積を求める ：
　　　　
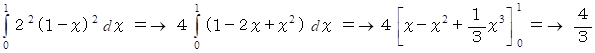
　　　　　　　底面より x の高さでの四角錐の水平断面は一辺が 2(1−x) の長さの正方形です。