正多面体とは、 １ 種類の合同な正多角形だけを面に持ち、 頂点に集まる面の数がどこも等しい多面体のことです。
　 正多面体のうち最も面の数が少ないのは正四面体で、 ４つの正三角形の面からなります。
　 一辺の長さが １ の正四面体の、 高さは 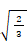であり、 隣り合う面が交わる角度は 約 70.53 度 です。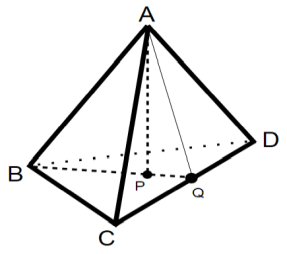

　　　　　

　 天頂点Ａから底面の正三角形ＢＣＤに対して下した垂線の交点をＰとし、 辺ＣＤの中点をＱとします。
　　　　　
　　　　　
　　　　　
　　　　　
　　　　　
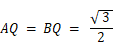
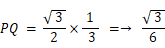
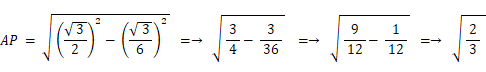
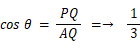
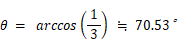
　 （ 参 考 ）
　　　　　　解析学 ＞ 正四面体の体積


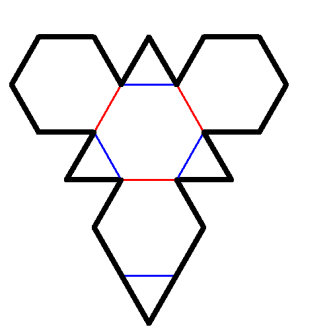
　 正四面体の４つの頂点を向かい合う面に平行になるように削ると正三角形の面ができます。 元々あった正三角形の面が正六角形になるまで４つの頂点を削ります。 こうして出来上がった ４つの正六角形の面 と ４つの正三角形の面 からなる多角形を「 切頂四面体 」と言います。 下に切頂四面体の展開図を示します。 青色の部分を 90° 山折りに、 赤色の部分を 110° 山折りにすると、 切頂四面体 になります。