(1) 力の定義
-
力学とは、 力 と 変位 と 力学的エネルギー に関する物理学です。 変位とは移動のことです。 力学的エネルギーは、 運動エネルギー と 位置エネルギー の総称のことで、 エネルギーとは、 仕事 ( 力を変位で積分したもの ) をする能力のことです。 では、 力とは何でしょうか? 力とは、 運動量を時間で積分したものです。 力の定義は、 結局、 運動方程式になります。
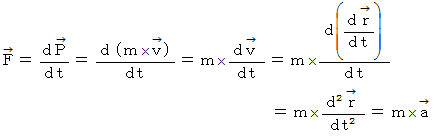
運動方程式の元々の概念は、 関数であり、 関数器の作用が「 力をかける 」で、 入力する物が「 質量 」で、 出力される物が「 加速度 」です。 運動量保存法則 や 力学的エネルギー保存法則 は、 運動方程式から導かれます。 力学の根本は、 運動方程式なのです。 したがって、 力学の問題は、 まず運動方程式を作ることから始まります。
運動方程式から運動量が発見されました。 それは、 両辺を時間で積分することによってです。
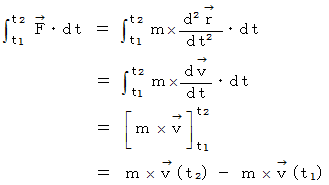
この式の左辺は、 力を時間で積分したもので、 力積 と言われます。 右辺は、 運動量の変化です。 先ほど述べました力の定義の前に、 この力積の概念があるものですから、 先ほどの力の定義はおかしんじゃないかとの見方もあり、 鶏が先か卵が先か状態になっています。
-
考えやすくするために、 摩擦や空気抵抗はなく、 一様な重力場
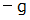 が存在する世界であるとします。 床の上に質量
が存在する世界であるとします。 床の上に質量 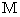 の三角台を置き、 質量
の三角台を置き、 質量  のボールを斜面の高さ
のボールを斜面の高さ 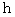 の所から、 静かに離して転がします。 下の図は、 ボールが転がっている最中の瞬間を捉えたシェーマです。 この時のボールの速度を
の所から、 静かに離して転がします。 下の図は、 ボールが転がっている最中の瞬間を捉えたシェーマです。 この時のボールの速度を 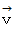 とします。 この時、 三角台も床に対して右向きの移動をしており、 その速度を
とします。 この時、 三角台も床に対して右向きの移動をしており、 その速度を 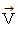 とします。
とします。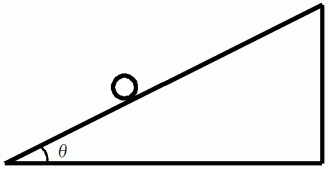
これから、 ボールと三角台の移動について考えてみましょう。 その考え方は次の手順によります。
1. それぞれに物質に作用している力をすべて図で表す。
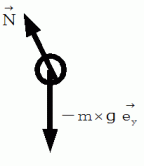
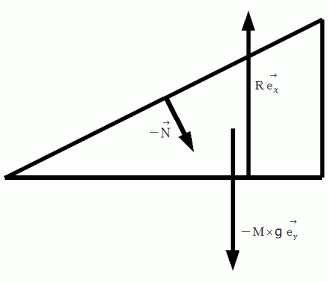
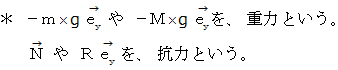
2. それらの力を合成する。
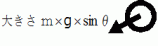
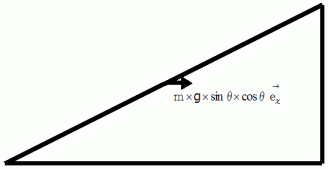
3. 合成された力を水平方向と垂直方向に分解する。
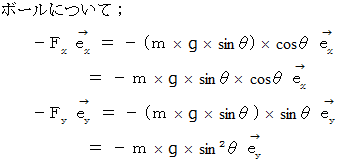
4. 合成力の水平方向成分を質量で割ると、 水平方向の加速度が求まり、 合成力の垂直成分を質量で割ると、 垂直方向の加速度が求まる。
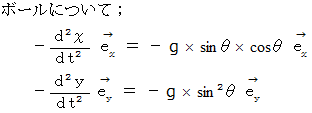
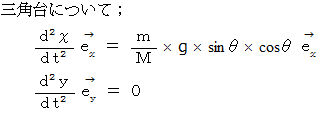
5. それぞれの物質の水平成分の運動方程式と垂直成分の運動方程式を作る。
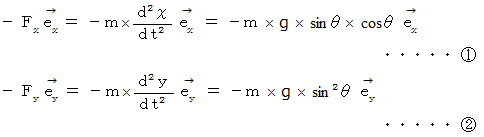
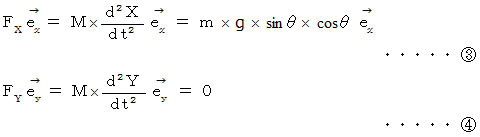
6. 最後に、 全体的なベクトル運動方程式を作る
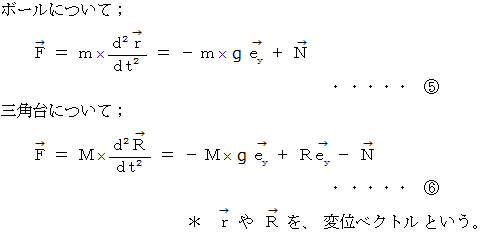
 力学 へ戻る
力学 へ戻る