2　　3　　7　　43　　1807　・・・・ という数列は、次のような式で表されます。


n＝1 を代入すると、
　　a₂ ＝ a₁ ＋ 1 ＝→ 2＋1 ＝→ 3
n＝2 を代入すると、
　　a₃ ＝ a₁ × a₂ ＋ 1 ＝→ 2×3＋1 ＝→ 7
n＝3 を代入すると、
　　a₄ ＝ a₁ × a₂ × a₃ ＋ 1 ＝→ 2×3×7＋1 ＝→ 43

さて、
　　
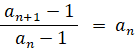
よって、
　　a_n+1−1 ＝ a_n²−a_n
よって、
　　a_n+1 ＝ a_n²−a_n＋1

したがって、　2　　3　　7　　43　　1807　・・・・ という数列は、次のような漸化式でも表されます。


この数列はシルベスター数列と言われます。


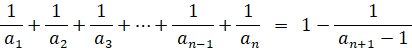
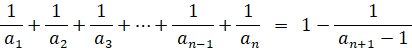
（ 証 明 ）

n＝1 のとき、以下のように上式は成り立つ。
　　
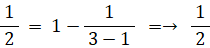
n＝k のとき上式は成り立つと仮定する。つまり、次の式が成り立つと仮定する。
　　
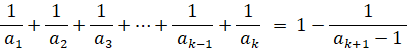
n＝k＋1 のとき、上式は、
　　
　　　　　　　　　　　　
　　　　　　　　　　　　
　　
　　　　　　　　　　　　
　　　　　　　　　　　　
　　　　　　　　　　　　
　　　　　　　　　　　　

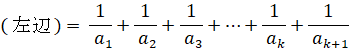
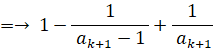
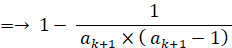
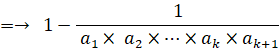
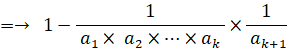
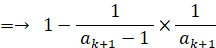
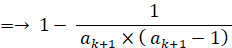
　 （ 左辺 ）＝（ 右辺 ）にて、n＝k＋1 のときも上式は成り立つ。

というわけで、数学的帰納法にて、上式は成り立つことが証明された。

【 問 題 】

1805/1806 を エジプト式分数 （ 単位分数の和の形 ） で表せ。

【 解 答 】

1 − 1/(1807−1)　＝→　1805/1806　だから、答えは次のようになる。
　　　1/2 ＋ 1/3 ＋ 1/7 ＋ 1/43