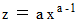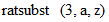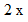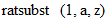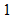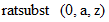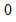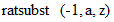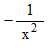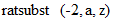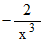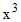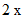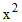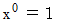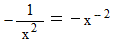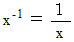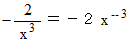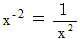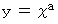
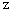が次の整数をとりながら変化するとき、 がどんな値をとるのか見てみましょう。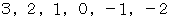
　　　　　

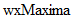　 を用います。 まず、 と入力します。 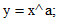ではありません。 次に、 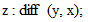と入力します。 すると、 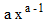と出力されます。 次に、 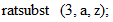と入力します。 すると、 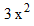と出力されます。 その次に、 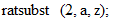と入力します。 すると、 。 このようにして得られた結果を表にします。

　 この表をよく見ていますと、 がどこにも登場していないことに気づきます。 多分次のようになって姿を消しているんだと思います。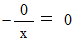
　　　　

この表の値を積分すれば元に戻るはずです。 やってみましょう。

確かに元に戻っています。


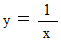　を微分してみましょう。 答えは次のようになります。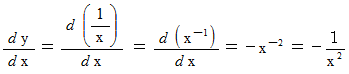
　　　　　
今度は、 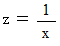　を積分してみましょう。 まずは失敗例です。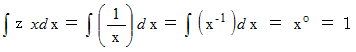
　　　　　
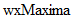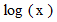　 では、 正解を に聞いてみましょう。 と入力します。 すると、 と出力されます。

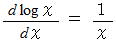　ならば、 次のようになります。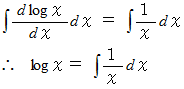
　　　　　

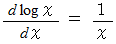　 　の証明というか定義というか、 それに関しましては、大学生のための数学 ＞ 三角関数 指数・対数関数 ＞ おいらの愛した波動方程式　の中の「（３）自然対数の起源 」 をご覧ください。