プログラムの内容 :
0以上1未満の小数第1位までの純小数を任意に2つ取り出す。 ( 例えば、 0.4 と 0.7 ) そして、 加えてから小数点以下を四捨五入したもの と 小数点以下を四捨五入してから加えたもの との大きさを比較する。 このことを十進BASIC のプログラムを作って行うことにした。 2つのプログラムを組んだが、 後者のほうがそのしくみを考えたアルゴリズムになっているので優秀なプロブラグラムだと思う。
実行の結果、 前者の方が後者よりも大きい確率 と 後者の方が前者よりも大きい確率が異なっていた。 実際の個数を数えると、 前者の方が後者よりも大きいのは 10ケース で 後者の方が前者よりも大きいのは 15ケース であった。 四捨五入の場合、 小数点第1位が 0, 1, 2, 3, 4 の場合が切り捨てで、 小数点第1位が 5, 6, 7, 8, 9 の場合が切り上げなので、 切り捨てになる確率と切り上げになる確率は等しい。 なのに、 これはいったいどういうことなのか?
そこで今度は、 0以上1未満の純小数を任意に2つ取り出して、 同様のことを行ってみることにした。 後者のプログラムを応用して、 次のようなグラフを作成する。
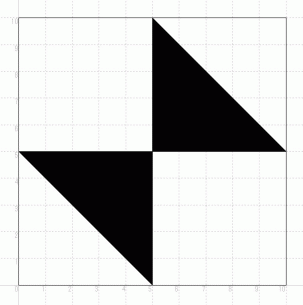
10 × 10 の正方形のうち、 黒く塗りつぶしたところが、 加えてから小数点以下を四捨五入したものと、 小数点以下を四捨五入してから加えたものの大きさが異なる範囲である。 それ以外が前者と後者が等しくなる範囲である。 したがって、 前者と後者が等しい確率は 75 % であり、 前者の方が後者よりも大きい確率 と 後者の方が前者よりも大きい確率 は、 ともに 12.5 % であることがわかった。
そこで、 最初の問題に戻ろう。
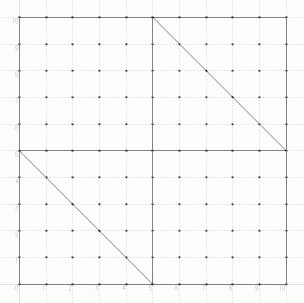
点( 0,5 ) と 点( 5,0 ) とを結ぶ線分上の点 ( 両端を除く )
前者 > 後者 が 4個
点( 0,5 ) と 点( 5,5 ) とを結ぶ線分上の点 ( 点( 5,5 ) を除く )
前者 = 後者 が 5個
点( 5,0 ) と 点( 5,5 ) とを結ぶ線分上の点( 点( 5,5 ) を除く )
前者 = 後者 が 5個
点( 5,10 ) と 点( 10,5 ) とを結ぶ線分上の点
前者 = 後者 が 6個
点( 5,5 ) と 点( 10,5 ) とを結ぶ線分上の点 ( 点( 10,5 ) を除く)
前者 < 後者 が 5個
点( 5,5 ) と 点( 5,10 ) とを結ぶ線分上の点 ( 両端を除く )
前者 < 後者 が 4個
したがって、
前者の方が後者よりも大きいのは、 4+6
 10 ケース
10 ケース後者の方が前者よりも大きいのは、 5+4+6
 15 ケース
15 ケース