（１） サークル内での回覧板的な商品売買

　 Ｎ 個 の椅子が円周上に等間隔に置かれています。 そこに千円を持った人が １ 人座っていて、 それ以外の椅子には、 各々が生産した千円の価格のする商品を持った人たちが座っています。 まず、 千円を持った人が隣の人から商品を買います。 すると、 商品を売った人は、 その千円を使って次の隣の人から商品を買います。 こういったことが ｍ 回 続いた後はどうなっているでしょうか？　千円を持った人から数えて ｋ 番名の人は、 全体で ｋ 回目の交換が行われた直後には千円を持っていることになります。 また、 ｍ ＜ Ｎ のときは、 元々持っていた商品を持ち続けている人が （ Ｎ−ｍ−１ ） 人 になります。

　 こんな状況を商品に注目して表現してみます。 千円を持っている人の席は空席と考え、 空席は動かないで、 交換のたびに円列になった商品たちが回転すると考えます。 千円を持ったいる人から数えて ｋ 番名の席の人が持っていた商品は、 ｍ 回目の交換が終わった直後に何度回転しているでしょうか？

　 その答えはこうです。

　　　　　AMAR （ ｍ ÷ Ｎ ）　≧　ｋ　の場合い ：
　　　　　　　　　｛ ｍ ＋ SYOU （ ｍ ÷ Ｎ ） ＋ １ ｝ × （ 360 ÷ Ｎ ）

　　　　　AMAR （ ｍ ÷ Ｎ ）　＜　ｋ　の場合い ：
　　　　　　　　　｛ ｍ ＋ SYOU （ ｍ ÷ Ｎ ） ｝ × （ 360 ÷ Ｎ ）

　　　　　　　　　　　　　　　　＊　SYOU （ a ÷ b ） ：　a を ｂ で割った商を表す
　　　　　　　　　　　　　　　　　　 AMAR （ a ÷ b ） ：　a を ｂ で割った余りを表す


　 次に、 視点を変えてみましょう。 椅子が９個のケースについて考えます。 千円を数字の １ で表し、 それ以降の商品を数字の ２、 ３、 ４、 ・ ・ ・　で表します。 また、 最初に千円を持っていた人を とし、 それ以降の人たちを 、 、 とします。 そこで、 この２つの数字の対応について見てみます。

　 まず、 ５回目の交換が行われた直後の状態を見てみましょう。
　　　　
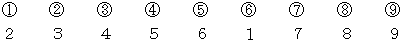
　 最初に持っていた物と変わってない人のことは無視して、 から ついて、 に対応している ２ と同じ を探し、 に対応している ３ と同じ を探し、 ・ ・ ・ ・ ・　というふうに繰り返してみてください。 最後は に帰ってきます。

　 次に、 ９回目の交換が行われた直後の状態を見てみましょう。
　　　　　
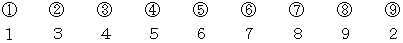
　 最初に持っていた物と変わってない人のことは無視して、 から ついて、 に対応している ３ と同じ を探し、 に対応している ４ と同じ を探し、 ・ ・ ・ ・ ・　というふうに繰り返してみてください。 最後は に帰ってきます。

最後に、 51 回目の交換が行われた直後の状態を見てみましょう。
　　　　　
　 最初に持っていた物と変わってない人のことは無視して、 から ついて、 に対応している ６ と同じ を探し、 に対応している ３ と同じ を探し、 ・ ・ ・ ・ ・　というふうに繰り返してみてください。 最後は に帰ってきます。

　 以上のように、 最初に持っていた物と変わってない人のことを無視して調査すると、 どんなケースについてもきれいに巡回していることが分かりました。

（２） 置換

　 数列　 　を 数列 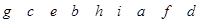　に変換することを、 次のように表すことにします。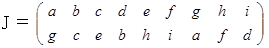
　　　　　
　 このような変換を 「 置換 」 と言います。 数列の等しい項に注目しますと、 それぞれの項が次のように変換されていると言うこともできます。
　　　　　

　置換の合成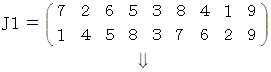

　　　　　
　　　　　
　　　　　
　　　　　
　　　　　
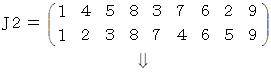
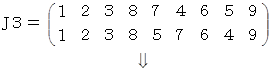
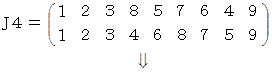
　　　　　　　　　　　　　　　　　　＊　 Ｊ１ 〜 Ｊ５ は 後述する 「 巡回置換 」 であり、
　　　　　　　　　　　　　　　　　　　　後述の８パズルの解を求めるものです。

　　　　　置換の合成を次のように表すことにします。
　　　　　　　　　　

　巡回置換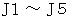

　 の置換を、配列にこだわらずに変換された数字たちにだけ着目して表しますと、 次のようになります。
　　　　　
　　　　　
　　　　　
　　　　　
　　　　　

　 すると、 これらの置換の共通点が見えてきます。 その共通点とは、 数字が変換されないグループ と 数字が変換されるグループ とに２分され、 数字が変換されるグループは順繰りに変換されているということです。 こういった置換を 「 巡回置換 」 と言います。

（３） ８スライドパズル

　 （２） の巡回置換の例は、 ある８パズルの解を求めるものです。 数字の９だけは、 空枠を表しています。

　　　

　　　　　　　　　

　　　　　　　　　　　　　　　　

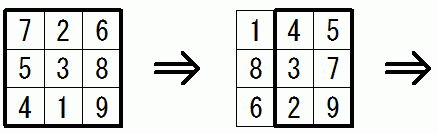
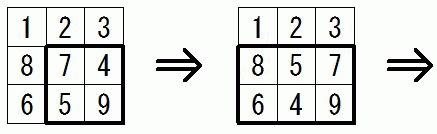
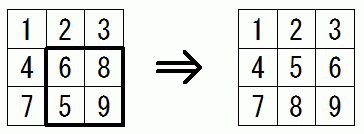
　　　　　　　　　　　※　実際には、 もっと早く完成することができます。
　　　　　　　　　　　　 ３番目の図から一気に成就できます。

　互換

たとえば次のように表される巡回置換は、「 互換 」といわれます。
　　　　　

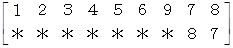
この互換の例は、 次のようなものです。
　　　　　

また、 次のように、 置換は互換の合成で表すことができます。

　　　　　

　　　　　

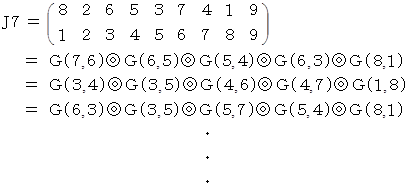
　 は互換が６個合成されたもので、 は互換が５個合成されたものです。 したがって、 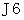のような置換は「 遇置換 」、 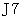のような置換は「 奇置換 」と言われます。

　 ８スライドパズルは 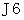のような遇置換では解が存在しますが、 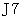のような置換は奇置換では解が存在しない そうです。

（４） ８スライドパズルが解ける確率

　３ × ３ 枠の最右最下の枠を空枠として、 １ 〜 ８ の数字を任意に８つの枠内に配置したとき、 そのスライドパズルが解ける確率を考えてみましょう。
　それには、「 解けて出来上がりになっている配列からペアの数を１組選ぶ場合の数 」と「 解けて出来上がりになっている配列から互換（ ２つの数字を選んでそれらを入れ替えること ） を１回したときの配列になる場合の数 」とを解明して計算すればいいのです。 しかし、 前者も後者も数が等しいことは自明ですから、 確率は ２分の１ であることがわかります。

　 これでいいのかどうかを確かめるために、 十進BASIC で次のようなシミュレーションプログラムを作ってみました。

JavaScript ＋ html のプログラム：

　 また、 ８スライドパズルが解けるかどうかを判定するプログラムは次のようになります。

JavaScript ＋ html のプログラム：