【 問題 1 】 ( 念願成就の期待値の基礎問題 )
-
1回転する毎に 0 〜 9 のうちどれか1個の整数を無作為に出力してくれる器械がある。
平均で何回転させると0を1回ゲットすることができるか?
-
1回転当たり0を1個ゲットする確率は 0.1 なので、「 0.1 × 1個 = 0.1 個 だから、1回転当たり0を得る期待値は常に 0.1 個である。」と考える。すると、「 0を1個獲得するためには、器械を10回転させる必要がある。」ということになる。 したがって、答えは 10 回転 である。
-
念願成就の期待値を E 回 とすると、 次の式が成り立つ。
E = 0.1 × 1 + 0.9 × ( 1 + E )
* 1回目に0が出る場合における期待値 と
1回目に0以外が出る場合における期待値 との 確率的加重平均
よって、 E = 10
-
一般に、 1 回試行あたりの念願成就確率を p とし、念願成就の期待値を S 回 とすると、 次の式が成り立つ。
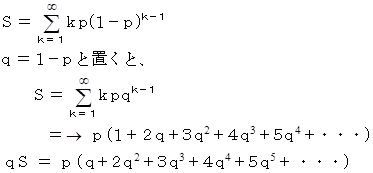
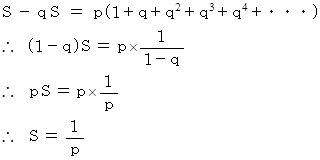
この公式に当てはめて、 答えは 10 回 となる。
プログラムの内容 :
【 問題 2 】 ( コレクション問題 その1 )
-
1 回転する毎に 0 〜 9 のうちどれか 1 個の整数をアットランダムに選出してくれる器械がある。 平均で何回転させると 0 〜 9 の全ての整数を揃えることができるか?
-
最初の 1 回転で新たな 0 〜 9 の整数をゲットする確率は 1 なので、 最初の整数を獲得する期待値を 1 にするためには器械を 1 回転させる必要がある。 2番目の整数をゲットする確率は 9/10 なので、 2番目の整数を獲得する期待値を 1 にするためには器械を 10/9 回転させる必要がある。 3番目の整数をゲットする確率は 8/10 なので、 3番目の整数を獲得する期待値を 1 にするためには器械を 10/8 回転させる必要がある。 4番目の ・ ・ ・ ・ ・ ・ 最後の整数をゲットする確率は 1/10 なので、 最後の整数を獲得する期待値を 1 にするためには器械を 10 回転させる必要がある。 というわけで、 すべての整数を揃える期待値を 1 にするためには、 必要な回転数の総和をとって、 次のようになる。
1 + 10/9 + 10/8 +10/7 + 10/6 + 10/5 + 10/4 + 10/3 + 10/2 + 10 ≒→ 29.29
次の10万回試行シミュレーションで確かめてみよう。
プログラムの内容 :
コレクション問題を漸化式を使って解く方法については、 確率 > 全ての種類が揃うまでの回数 をご覧ください。
【 問題 3 】 ( コレクション問題 その2 )
-
1 回転する毎に 0 〜 9 のうちどれか 1 個の整数をアットランダムに選出してくれる器械がある。 平均で何回転させると 5以下の数と6以上の数を少なくとも 1 つ以上ずつ揃えることができるか?
-
1 回転で 0 〜 5 の整数をゲットする確率は 3 / 5 であり、 6 〜 9 の整数をゲットする確率は 2 / 5 である。 よって、 0 〜 5 の整数が出るまでの期待値は 5/3 回 であり、 6 〜 9 の整数が出るまでの期待値は 5/2 回 である。 したがって、 求める答えは、
3 / 5 × ( 1 + 5 / 2 ) + 2 / 5 × ( 1 + 5 / 3 ) =→ 19 / 6( 回 )
※ 1回転目に5以下の数をゲットした場合の期待値 と
1回転目に6以上の数をゲットした場合の期待値 との 確率的加重平均
次の10万回試行シミュレーションで確かめてみよう。
 確率 へ戻る
確率 へ戻る