（ 問 題 ）

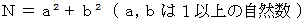　 の形で表される２よりも大きい素数 は、 ４ で割ると １ 余ることを証明しなさい。　（ フェルマーの２平方の定理 ）

（ 証 明 ）

　 も も偶数の場合、 または、 も も奇数の場合、 は偶数であるから素数ではない。 したがって、 か かのどちらかが偶数でどちらかが奇数であることが必要条件である。 そこで次のように置くと、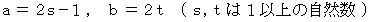
　　　　　
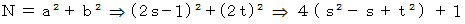　となる。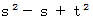
は自然数であるから、 は ４ で割ると １ 余ることが解る。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（ 証明終わり ）

　 さて、 以上の結果を早合点して次のように考えるのは、 逆は必ずしも真ならずで、 間違いです。
　　 　「 ４ で割ると １ 余る素数 は、 必ず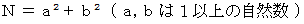
　　　　の形で表すことができる。」

　 しかし、 結果的には、 この命題は真になっていて 「 フェルマーの２平方の定理 」 と言われますので、 それでいいのですが、 論理的には間違いです。 そこで、 フェルマーの２平方の定理を証明したいのですが、 それはなかなか困難です。 そこで、 次のような十進BASIC のプログラムたちを作って、 5000 までの数について調べてみました。

　 実部と虚部がともに整数である複素数をガウス整数と言います。 ガウス整数 z が、 約数として８個の自明な約数　±1,　±i,　±z,　±iz　しか持たないとき、 z は ガウス素数 であるといいます。
　 実数または虚数のみでなるガウス整数については、 その大きさが ４ で割ると ３ 余る素数で表されるものがガウス素数であり、 実数と虚数の両方からなるガウス整数 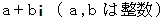については、 ノルム （ 大きさの２乗 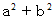：　　） が素数であるものがガウス素数です。 これもガウス素数の定義と言っていいでしょう。

　 ノルムが１００以下でガウス平面の第１象限に存在するガウス素数をすべて表示するプログラムを次に示します。

　　このプログラムソースは、 山中和義 / 電脳遊戯団 さんよりいただきました。
　　　　　http://www.urban.ne.jp/home/kz4ymnk/seminar/basic/