（１） ある不等式の証明から

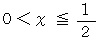　 　のとき、 次の式が成り立つことを証明しましょう。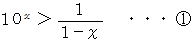
　　　　　

マクローリン展開より
　　　　　
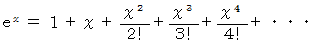
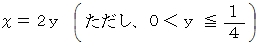　　　　　　と置くと、 次の式が成り立ちます。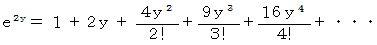
　　　　　
したがって、 次の式が成り立ちます。
　　　　　
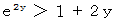
両辺に 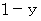をかけます。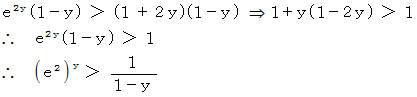
　　　　　
ここで、 であるから、
　　　　　

（２） 素数が無限にあることを証明したオイラー

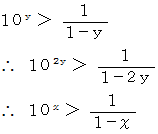
オイラー積 ：
　　　　　
　　　　　　　　 数理論 ＞ すべての積が登場するオイラー積　を参照ください。

より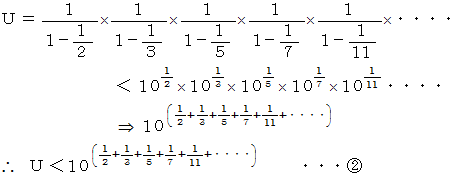
　　　　　

ここで、次のように置きます。
　　　　　
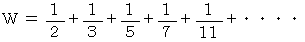
　 もし 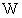が有限であると仮定すると、 式 は、 左辺が無限大で右辺が有限であるので、 無限大 ＜ 有限　となり、 矛盾します。 したがって、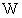 は無限大であると言えます。
　　　　　　　　　数理論 ＞ 平方数の和　を参照ください。

　こうして、 素数の逆数の和が無限大になることを証明したオイラーは、「 したがって、 素数は無限にあるのだ。」と言ったのです。
　 もし、 素数に最大の数があると仮定するならば、 全ての素数を掛け合わせた数に １ を加えた数は、 最大の素数よりも大きな素数となるので、 最初の仮定が間違っていたことになり、 素数には最大の数がないと言えます。 ということは、 素数は無限に存在するということです。