先日ＮＨＫで放映された番組 「 白熱教室海外版　オックスフォード白熱教室　第１回 『 素数の音楽を聴け 』　( 講師 ： マーカス・デュ・ソートイ教授 ) 」 は面白かった。 素数の数のリーマン予想のところは、 難しかったけれど、 波の重ね合わせの原理を用いることによって正確な予想に近づいていくという研究に度肝を抜かれた。 量子力学に類似している。
　　　　　
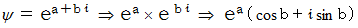
　 上記の波の方程式では、 振幅は で表され、 角振動数は で表される。 「 ゼータ関数の非自明なゼロ点 」 が　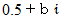　の形で表されるというのが 「 リーマン予想 」 で、 ゼータ関数の非自明なゼロ点を波の重ね合わせのようにしていくと、 「 数の原子 」 と言われる素数の分布状態が見えてくるということであった。 ゼータ関数は次のような関数である。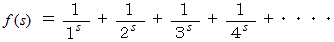
　　　　　
　 これを複素数の世界まで拡張するときには、 ガンマ関数も必要になってくるようで、 今の私にはそから先は真っ暗闇である。

　 次のような、 ある自然数以下の素数の数を大まかに近似する式が紹介されたので、 とりあえず、 これに基づいてプログラムを組んでみた。