【 問 題 】

次のような△ABCがある。
　　　
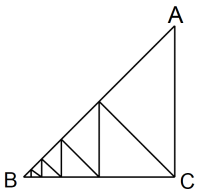
　　　　　　AC ＝ BC ＝ 1
　　　　　　∠C ＝ 90°

　頂点Cを出発して辺ABに向かって常に垂直な方向に進み、辺ABに達すると今度は辺BCに向かって常に垂直な方向に進み、辺BCに達すると今度は辺ABに向かって常に垂直な方向に進み ・・・ というふうに進んでいく。出発してから 2n 回目の方向転換をする瞬間までの道のりを f(n) とし、f(n) を n を用いて表せ。 また、１ 秒間に 1 の距離移動する速さで進むとき、頂点Cを出発してから何秒後に点Bに到達するかを示せ。

【 解 答 】

f(1) ＝ (1/2) ( root(2) ＋ 1 )
f(2) ＝ f(1) ＋ (1/2) f(1) ＝→ (1/2) ( root(2) ＋ 1 ) ＋ (1/2)² ( root(2) ＋ 1 )
f(n+1) − f(n) ＝ (1/2) { f(n) − f(n-1) }
h(n) ＝ f(n+1) − f(n) と置くと、
　　h(1) ＝ f(2) − f(1) ＝ (1/2)² ( root(2) ＋ 1 )
　　h(n) ＝ (1/2) h(n-1)
よって、 h(n) ＝ (1/2)² ( root(2) ＋ 1 ) (1/2)^n-1

h(1) ＝ f(2) − f(1)
h(2) ＝ f(3) − f(2)
h(3) ＝ f(4) − f(3)
　　　　　・
　　　　　・
h(n) ＝ f(n+1) − f(n)

辺々足すと、
　　h(1) ＋ h(2) ＋ h(3) ＋ ・・・ ＋ h(n)　＝　f(n+1) − f(1)
よって、
　　f(n+1) − (1/2) ( root(2) ＋ 1 )　＝　h(1) ＋ h(2) ＋ h(3) ＋ ・・・ ＋ h(n)
　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　
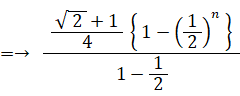
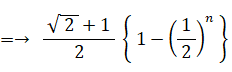
したがって、
　　
　　　　　　　
　　　　　　　
　　　　　　　
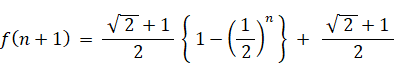
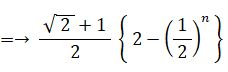
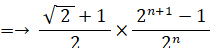
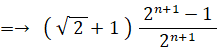
よって、
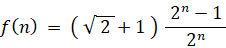　　　　　←（ 答え その１ ）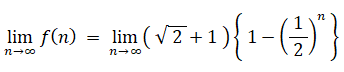

　　　　　
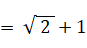
したがって、 ( root(2) ＋ 1 ) 秒後に点Bに到達する。（ 答え その２ ）