１ ： x の相似比 を持つ２つの相似な図形を、 同じ方向にして並べます。 すると、 ２つの図形の対応する２点を結ぶ直線は１点で交わります。

　　　　

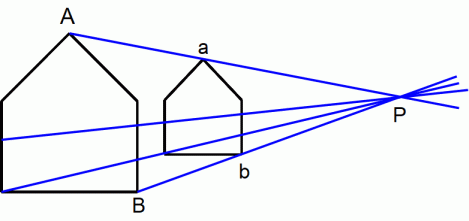
　 上図では次の式が成り立ちます。
　　　　
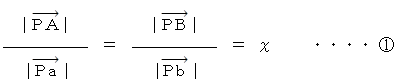
　 「 ２つの図形は点Ｐを中心として相似の位置にある。」 という表現をします。


　 では、 ２つの図形を反対方向に並べた場合はどうでしょうか？

　　　　

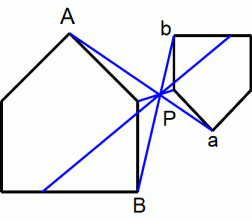
　 この場合も、 ２つの図形の対応する２点を結ぶ直線は１点で交わります。 そして、 式 が成り立ちます。 そして、２つの図形が合同なとき、点Ｐは２つの図形系の回転中心になります。


　 では、 ２つの図形を同じ方向でもなく反対方向でもなく並べた場合はどうでしょうか？

　　　　

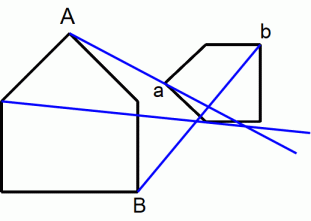
　 この場合は、 ２つの図形の対応する２点を結ぶ直線は１点で交わりません。