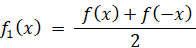
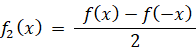
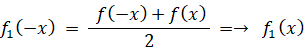 だから、f1(x) は 偶関数 である。
だから、f1(x) は 偶関数 である。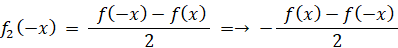
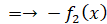 だから、f2(x) は 奇関数 である。
だから、f2(x) は 奇関数 である。※ 偶関数のグラフは y 軸に対して対称です。偶関数の代表は cos x
※ 奇関数のグラフは 原点を中止に180°回転させると元のグラフに重なります。奇関数の代表は sin x
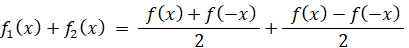
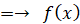
つまり、
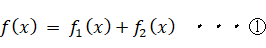
したがって、
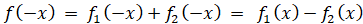
つまり、
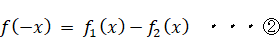
① と ② を辺々かけて、
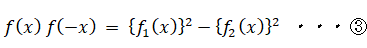
ここで、3つの関数を次のように置く。
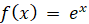
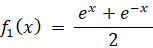
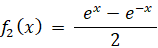
すると、
① より
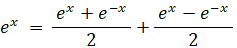
② より
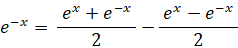
③ より
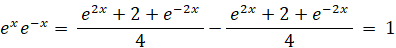
実は、
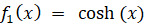 かつ
かつ 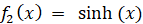
※ cosh (x) は ex と e-x で作られる 偶関数
※ sinh (x) は ex と e-x で作られる 奇関数
① より
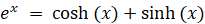 ← ※ この式が本質
← ※ この式が本質② より
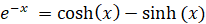
③ より
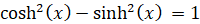
この式は 双曲線: x2-y2 = 1 を表している、
 その他の数学 へ戻る
その他の数学 へ戻る