（１） 虚数が取り持つ三角関数と指数関数の縁

　　　　
したがって、
　　　　
したがって、
　　　　

（２）　双曲線は虚数の匂いがする

楕円の方程式 ：
　　　　

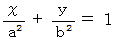
これは双曲線です。

（３） 半径 の扇形の中心角と面積の関係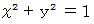

　 　は、原点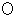 を中心とする、 半径 、面積 の円を表す方程式です。 次の図のように、 円周 と 軸の正の部分との交点を とし、円周上に点 をとり、 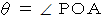とします。 すると、 となり、 扇形 の面積は になります。

　図−１
　　　　

（４） 双曲線関数

　図−２
　　　　
　 双曲線 ：　　の上にあって、 図−２ の灰色で塗りつぶされた部分の面積が になるような 点 を次のように表すことにします。 これが、 双曲線関数 と 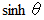の定義です。

　　　　

　 を原点を中心に反時計回りに４５度回転させると、 次のようになります。
　　　　
したがって、
　　　　
したがって、 　はそれぞれ次のように変換されます。
　　　　

これを 図−３ に示します。

　図−３
　　　　　　

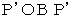　 で囲まれた部分の面積は、 で囲まれた部分の面積と で囲まれた部分の面積とを加えたものに等しいです。 また、 で囲まれた部分の面積は、 で囲まれた部分の面積と で囲まれた部分の面積とを加えたものにも等しいです。


　 したがって、 で囲まれた部分の面積は、 で囲まれた部分の面積に等しい。 で囲まれた部分の面積は、 次のような積分によって求めることができます。
　　　　
　　　　
　 したがって、 で囲まれた部分の面積は であり、 これは 図−２ の灰色で塗りつぶされた部分の面積に等しいので、 次の式が成り立ちます。
　　　　
　　　　
したがって、
　　　　

したがって、次の式が成り立ちます。
　　　　
この式たちより、 双曲線関数は三角関数の複素数への拡張であることがわかります。