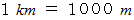は次のような物語を語っています。

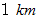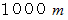　　　　　「 　は　　に等しい。」

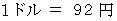　 　　は次のような物語を語っています。

　　　　　「 １ドル　は　９２円　に等しい。」

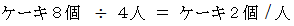　 　　は次のような物語を語っています。

　　　　　「 ケーキ８個　を　４人　で分けると、 一人当たり　ケーキ２個　になる。」

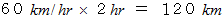　 　　は次のような物語を語っています。

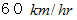　　　　　「 の速さで　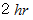　移動すると、　　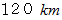変位する。」


　 こうしてみますと、 同じイコールでも意味合いが２つあることに気づきます。 そこで、 イコールの意味をイメージしやすい記号に置き換えて表すと、 次のようになります。

　　　　　

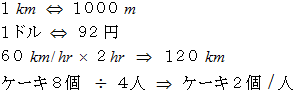
前者は天秤的なイコールであり、後者は演算的なイコールです。


では、 次の式の物語を語ってみてください。
　　　　

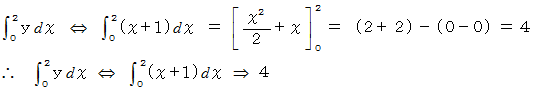
答えは、 次のようになります ：
　「 直交座標系において、 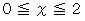の範囲で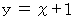、 直線 と 直線 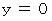とによって挟まれる部分の面積を求めるために、 微小面積 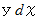の総計を求めると、 ４ になる。」

　 上記の式のイコールは単なる計算過程を表しています。 そこで、 次のような記号を用いて表すことにします。
　　　　


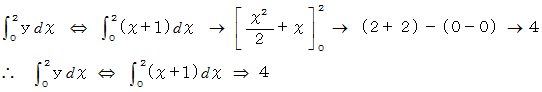
では次に、次の式の物語を語ってみてください。
　　　　　

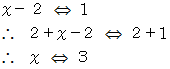
答えは、 次のようになります：
　「 は １ に等しい。 したがって、 両方に ２ ずつ加えた値も等しい。 前者に ２ を加えると になり、 後者に ２ を加えると ３ になる。 したがって は ３ に等しいことが解る。」


次の式の物語を語ってみてください。
　　　　　

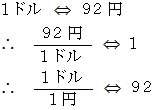
答えは、 次のようになります ：
　「 １ドル は ９２円 に等しい。 したがって、 ９２円 の １ドル に対する比率は １ に等しい。 したがって、 １ドル の １円 に対する比率は ９２ に等しい。」


次の式の物語を語ってみてください。
　　　　　

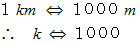
答えは、 次のようになります ：
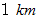　「 　は 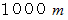に等しい。 したがって、 は １０００ に等しい。」


以上、 式の物語を語ることによって、 それらの本質が見えてくることがわかりました。