(4) ベクトルとしての複素数
-
比率の等式は、 次にように表されます。
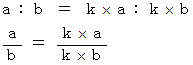
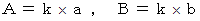 と置くと、 次のようになります。
と置くと、 次のようになります。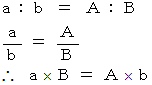
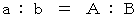 は、 「
は、 「  に対する
に対する  の姿は、
の姿は、 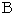 に対する
に対する  の姿に等しい。」 ということを表しています。 たとえば、 相似な3角形のペア
の姿に等しい。」 ということを表しています。 たとえば、 相似な3角形のペア 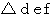 と
と 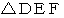 があるとき、 「
があるとき、 「 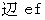 に対する
に対する 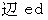 の姿は、
の姿は、 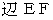 に対する
に対する 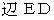 の姿に等しい。」 ということができ、 次のように表されます。
の姿に等しい。」 ということができ、 次のように表されます。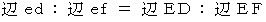
この式は、 次の2つのことを表しています。
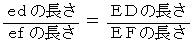
また、 ∠def = ∠DEF です。
ここで、 点
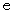 と 点
と 点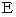 は重なっていて、
は重なっていて、 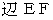 は、
は、 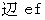 に対して、 反時計回りに、
に対して、 反時計回りに、 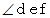 よりも大きく、 かつ、 90度以下の角をなしているものとします。 つまり、 次の不等式が成り立っているものとします。
よりも大きく、 かつ、 90度以下の角をなしているものとします。 つまり、 次の不等式が成り立っているものとします。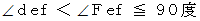
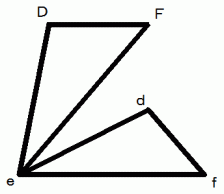
そして、
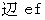 を基準になるものとし、 長さ
を基準になるものとし、 長さ  、 角度
、 角度  、 の線分であるとします。 すると、 次のようになります。
、 の線分であるとします。 すると、 次のようになります。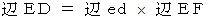
この式は、 次の2つのことを示しています。
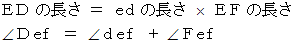
これは、
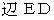 の、 基準になる
の、 基準になる 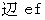 に対する姿を表しています。 長さは乗法になっており、 角度は加法になっているところに注目してください。
に対する姿を表しています。 長さは乗法になっており、 角度は加法になっているところに注目してください。 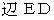 は
は 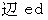 と
と 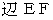 をかけ合わせたものです。 角度とは方向を表すものですから、 この場合、 辺はベクトルであると言えます。 そこで、
をかけ合わせたものです。 角度とは方向を表すものですから、 この場合、 辺はベクトルであると言えます。 そこで、 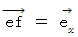 ,
, 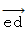 ,
, 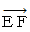 ,
, 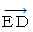 として、 「
として、 「 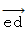 に
に 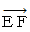 をかけるという演算をすると
をかけるという演算をすると 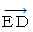 になる。」 とします。 ということは、「
になる。」 とします。 ということは、「 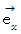 に
に 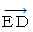 をかけるという演算をすると
をかけるという演算をすると 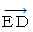 になる。」 と言うことができます。 これらのことを、 それぞれ、 次のように表すことにします。
になる。」 と言うことができます。 これらのことを、 それぞれ、 次のように表すことにします。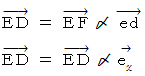
ここで、 単位ベクトル
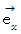 に対して、 反時計回りに90度回転した単位ベクトルを、
に対して、 反時計回りに90度回転した単位ベクトルを、 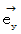 とします。
とします。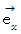 に対して
に対して 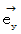 を内積させたもの に対して、
を内積させたもの に対して、 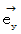 を内積させると、
を内積させると、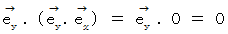
 に対して
に対して  を外積させたもの に対して、
を外積させたもの に対して、  を外積させると、
を外積させると、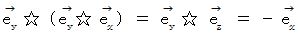
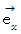 に対して
に対して 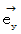 をかけたもの に対して、
をかけたもの に対して、 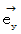 をかけると、
をかけると、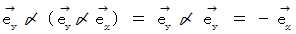
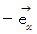 に対して
に対して 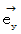 をかけたもの に対して、
をかけたもの に対して、 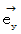 をかけると、
をかけると、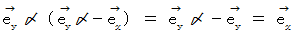
演算子
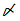 において、
において、 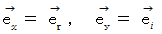 と置き直します。 そして、 この直交する2つの基底の要素たち
と置き直します。 そして、 この直交する2つの基底の要素たち 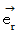 と
と 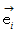 で形成されるベクトル空間を、 複素平面( ガウス平面 )と言います。
で形成されるベクトル空間を、 複素平面( ガウス平面 )と言います。 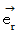 と
と 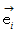 との間には、 次のような演算が成立します。
との間には、 次のような演算が成立します。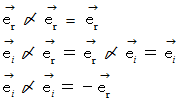
このベクトル空間に次のようのベクトルがあるとします。
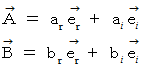
すると、
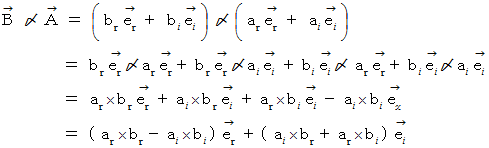
さて、 次のような条件があるとき、
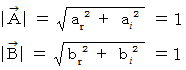
それぞれのベクトルは、 極形式を用いて、 次のように表されます。
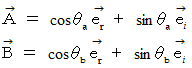
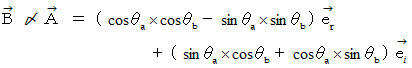
一方、 オイラーの公式より、
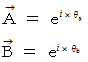
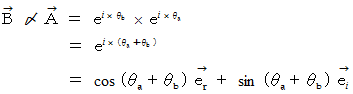
この式に、 次の三角関数の加法定理を代入すると、
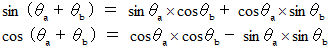
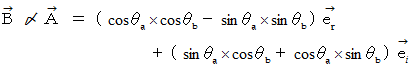
 この論文のトップ へ戻る
この論文のトップ へ戻る