(1) 数学的手法としての複素数
-
物理学においては、 複素数数が数学的手段として使用され、 それによって、 比較的簡単に、 求めたい物理量に辿り着くことができます。 例えば、 次のようなものです。
1. 相対性理論
-
特殊相対性理論では、 「 時間という物理量 」 や 「 角度という数 」 が虚数であると考えることによって、 「 ローレンツ変換 」 が 「 回転という等長変換 ( 合同変換 ) 」 と同等なものになり、 論理性が保たれます。 ただし、 ここで言う 「 論理性が保たれる 」 とは、 「 ニュートン力学的な観察 」 が 「 相対論的な観察 」 に翻訳されたときに、 時間や距離が変化しない、 という意味です。 実数のみの 「 ローレンツ変換 」 では、 「 ニュートン力学的な観察 」 が 「 相対論的な観察 」 に翻訳されたときに、 時間や距離が変化してしまいます。
-
複素数をベクトルとして取り扱います。 つまり、 複素平面 ( ガウス平面 ) で表される2元数としての複素数を利用します。 そうすることによって、 位相のズレが簡単に表現できます。 位相のズレは、 複素数ベクトルどうしのかけ算で表現することができるようになり、 複素平面上では、 反時計回りの回転としてイメージができるようになります。
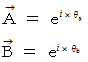
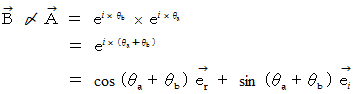
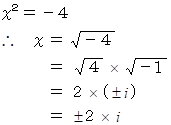
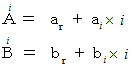
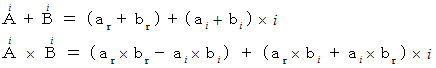
(3) 虚数角
オイラーの公式より、
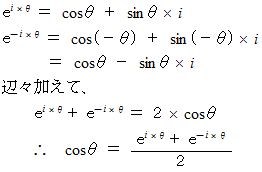
この式から、 虚数角の余弦は次のように定義される。
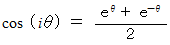
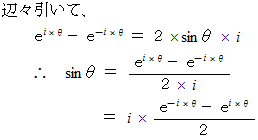
この式から、 虚数角の正弦は次のように定義される。
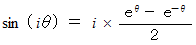
 数理論 へ戻る
数理論 へ戻る