三角形の各頂点から対辺に垂直に下ろした線分は１点で交わり、その点を垂心といいます。
三角形の各頂点から対辺に垂直に下ろした線分は１点で交わることを証明してみましょう。
そのためには、下図の ∠BFC が 90 度 であることを証明すればいいのです。

　　　　

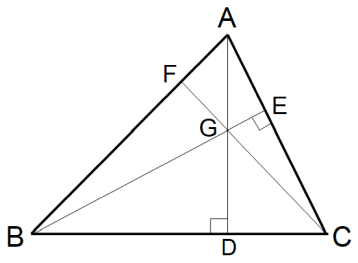
では、やってみましょう。

　　　　

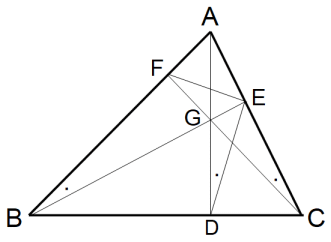
円周角の定理（ 弧AB： ∠AEB ＝ ∠ADB ） より、点A,B,D,E は同一円周上にある。
円周角の定理（ 弧CG： ∠CEG ＝ ∠CDG ） より、点G,D,C,E は同一円周上にある。
点A,B,D,E は同一円周上にあるので。円周角の定理（ 弧AE ）より、 ∠ABE ＝ ∠ADE
点G,D,C,E は同一円周上にあるので。円周角の定理（ 弧GE ）より、 ∠GDE ＝ ∠GCE
∠ADE ＝ ∠GDE より、∠ABE ＝ ∠GCE
∠ABE ＝ ∠FBE と ∠GCE ＝ ∠FCE より、∠FBE ＝ ∠FCE
円周角の定理（ 弧FE： ∠FBE ＝ ∠FCE ） より、点F,B,C,E は同一円周上にある。
円周角の定理（ 弧BC ）より、 ∠BFC ＝ ∠BEC
∠BEC ＝ 90 度 なので、∠BFC ＝ 90 度

以上で証明終わりです。