（１） 広島大学の過去の入試問題より

（ 問 題 ）
　 一辺の長さが２の正三角形の内部に任意に５つの点をとる。 このとき、 ２点間の距離が１以下のペアが必ず存在することを証明せよ。


（ 解 答 ）
　 一辺の長さが２の正三角形は、 下図のように一辺の長さが １ の正三角形４つに分割することができる。

　　　　　　　

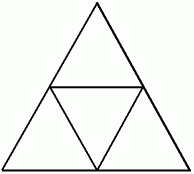
　 鳩の巣原理より、 ５点のうち少なくとも２点は同じ小三角形の内部または辺上に存在する。 一辺の長さが １ の正三角形の内部または辺上に存在する２点の距離は １ 以下なので、 題意は満たされる。

（２） 神戸大学の過去の入試問題より

（ 問 題 ）
　 相異なる４つの整数から２つの整数をうまく選ぶと、 その差が３の倍数になることを証明せよ。


（ 解 答 ）
　 整数を次の３つの群に分ける。 （ k は整数 ）
　　　　　Ａ群 ：　3k
　　　　　Ｂ群 ：　3k+1
　　　　　Ｃ群 ：　3k+2

　 相異なる４つの整数が与えられたとき、 鳩の巣原理より、 少なくとも１組は同じ群に属する。 同じ群に属する整数の差は３で割り切れるから、 題意は満たされる。