（１）　等差数列と等比数列とのコラボ

　　　　　

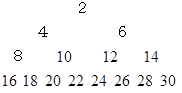
　 上の図のように、 ４行にわたり数字が配置されています。 この法則に従って数字がずっと並べられていった場合、 第 ｎ 行目の一番最後の数 と それまでの数の総和は、 それぞれいくらになるでしょうか？

　 まず、 第 ｎ 行までに数字が全部で何個あるのかを調べてみましょう。 それには、 次のようにすべての数を １ に置換して考えると容易になりそうです。

　　　　　

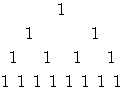
　 ｎ 行目の １ の個数を 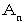、ｎ 行目までの １ の総個数を 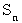とします。 すると、 初項が １ 、 公比が ２ の 等比数列の公式より、 次のようになります。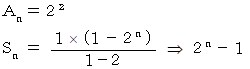

　　　　　

　 したがって、 第 ｎ 行目の一番最後の数は、 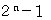番目の数であることが解ります。

　 ｍ 番目の数を 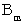　 、 ｍ 番目の数までの総和を 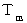とします。 すると、 初項が ２ 、 公差が ２ の 等差数列の公式より、 次のようになります。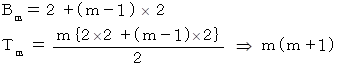

　　　　　

　したがって、 第 ｎ 行目の一番最後の数 と それまでの数の総和 は、 それぞれ次のようになります。

　　　　　

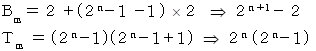
　 こういった数列は「 群数列 」と言われ、1999年度のセンター試験でも出題されています。

（２）　等差数列と等差数列とのコラボ

（ 問 題 ）
奇数が小さい順に並んだ数列がある。
小さい方から順に、 ２個、４個、６個、８個、 ・ ・ ・ ・　と、 仕切りで区切って、 第１群、 第２群、 第３群、 第４群、 ・ ・ ・ ・ 　と分けていく。

１　３　｜　５　７　９　11　｜　13　15　17　19　21　23　｜　25　27　29　31　33　35　37　39　｜　41　43　45　・ ・ ・ ・ ・

　（１） 第ｎ群の最初の数を述べよ

　（２） 第ｎ群の個数を述べよ


（ 解 答 ）

　　　　基本の数列 ：　１　３　５　７　９　11　・ ・ ・ ・　　（ 初項 １ 公差 ２ の等差数列 ）
　　　　群の個数の数列 ：　２　４　６　８　10　・ ・ ・ ・　　（ 初項 ２ 公差 ２ の等差数列 ）

　　　　基本の数列の第 ｎ 項　＝　２ｎ−１
　　　　基本の数列の第 ｎ 項までの和　＝　ｎ^２
　　　　群の個数の数列の第 ｎ 項　＝　２ｎ
　　　　群の個数の数列の第 ｎ 項までの和　＝　ｎ (ｎ＋１)

（１）
第 １ 群の最初の数は １ である。
これから、第２群以降について考察する。
第 ｎ 群の最初の数は、基本の数列の第 （ 群の個数の数列の第 ｎ−１ 項までの和に １ を足した数 ） 項の数である。
群の個数の数列の第 ｎ−１ 項までの和に １ を足した数とは、
　　　　　( n − １ ） ｎ ＋ １　 ＝→　 ｎ^２ − ｎ ＋ １
よって、第ｎ群の最初の数は、基本の数列の第 （ ｎ^２ − ｎ ＋ １ ） 項の数である。
基本の数列の第 （ ｎ^２ − ｎ ＋ １ ） 項の数とは、
　　　　　２ （ ｎ^２ − ｎ ＋ １ ） − １　 ＝→　 ２ｎ^２ − ２ｎ ＋ １
したがって、 第 ｎ 群の最初の数は　２ｎ^２ − ２ｎ ＋ １　である。
ｎ ＝ １　のとき、 ２ｎ^２ − ２ｎ ＋ １　＝　１　となるので、 答えは、 次のようになる。
　　　　　２ｎ^２ − ２ｎ ＋ １

（２）
第 ｎ 群の初項は、 ２ｎ^２ − ２ｎ ＋ １
第 ｎ 群の終項は、 ２（ ｎ ＋ １ ）^２ − ２（ ｎ ＋ １ ） ＋ １
　　　　　　　　　　　　　＝→ 　２ｎ^２ ＋ ２ｎ − １
第 ｎ 群の項数は、 ２ｎ

したがって、 第 ｎ 群の数の合計は、
　　　[｛（ ２ｎ^２ ＋ ２ｎ − １）　−　（ ２ｎ^２ ＋ ２ｎ − １ ）｝　×　２ｎ ]　÷　２
　　　　＝→　４ｎ^３

（２） の別解

　第 ｎ 群の数の合計は、 基本の数列の第（ 群の個数の数列の第 ｎ 項までの和 ）項までの和 から 基本の数列の第（ 群の個数の数列の第 ｎ−１ 項までの和 ）項までの和 を引いた数である。
　基本の数列の第（ 群の個数の数列の第 ｎ 項までの和 ）項までの和 とは、 基本の数列の第 ｎ(ｎ＋１) 項までの和だから、 ｎ^２（ ｎ ＋ １ ）^２　である。
　基本の数列の第（ 群の個数の数列の第 ｎ−１ 項までの和 ）項までの和 とは、 基本の数列の第 ｎ(ｎ−１) 項までの和だから、 ｎ^２（ ｎ − １ ）^２　である。
よって、 第 ｎ 群の数の合計は、
　　　ｎ^２（ ｎ ＋ １ ）^２　−　ｎ^２（ ｎ − １ ）^２　＝→　ｎ^２｛（ ｎ ＋ １ ）^２　− （ ｎ − １ ）^２
　　　　＝→　 ４ｎ^３