【 問 題 】
-
次の数列の第 n 項までの和を求めよ。
1 2 k 3 k 2 4 k 3 ・・・・ n k n−1
※ ただし、k は 1 以上の整数
-
求める値を S とすると、
S = 1 + 2 k + 3 k 2 + 4 k 3 + ・・・・ + n k n−1
k = 1 のとき、
S = 1 + 2 + 3 + 4 + ・・・・ + n
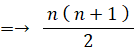
k > 1 のとき、
-
k S = k + 2 k 2 + 3 k 3 + 4 k 4 + ・・・・ + n k n
S − k S = 1 + k + k 2 + k 3 + ・・・・ + k n−1 − n k n
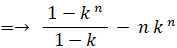
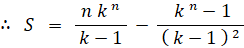
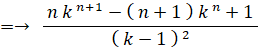
 数理論 へ戻る
数理論 へ戻る