自然数の集合は、 加法について閉じている。
加法とは、 ある数を入力すると、 決められた数だけ増やされた数を出力する演算である。
しかし、 自然数の集合は、 減法について閉じていない。
減法とは、 ある数を入力すると、 決められた数だけ減らされた数を出力する演算である。
そこで、 自然数は整数に含まれるとし、 数の世界は整数まで拡張された。
整数の集合は、 減法についても閉じている。
加法とは、 ある数を入力すると、 決められた数だけ増やされた数を出力する演算である。
しかし、 自然数の集合は、 減法について閉じていない。
減法とは、 ある数を入力すると、 決められた数だけ減らされた数を出力する演算である。
そこで、 自然数は整数に含まれるとし、 数の世界は整数まで拡張された。
整数の集合は、 減法についても閉じている。
整数の集合は、 乗法について閉じている。
乗法とは、 ある数を入力すると、 決められた回数だけその数を加えた数を出力する演算である。
しかし、 整数の集合は、 除法について閉じていない。
除法とは、 ある数を入力すると、 決められた数を何個加えればその数になるのかを出力する演算である。
そこで、 整数は有理数に含まれるとし、 数の世界は有理数まで拡張された。
有理数の集合は、 除法についても閉じている。
乗法とは、 ある数を入力すると、 決められた回数だけその数を加えた数を出力する演算である。
しかし、 整数の集合は、 除法について閉じていない。
除法とは、 ある数を入力すると、 決められた数を何個加えればその数になるのかを出力する演算である。
そこで、 整数は有理数に含まれるとし、 数の世界は有理数まで拡張された。
有理数の集合は、 除法についても閉じている。
ここまでならば、 ある演算について閉じていないからという理由で、 数の概念がどんどん拡張されていった歴史がわかります。 しかし、 無理数への拡張は違います。 では、 無理数の概念はどこからきたのでしょうか?
辺の長さが 1 の正方形の対角線の長さは 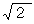 であるが、
であるが、
これが分数では表すことのできない無限小数であることが証明され、
有理数は数直線上にとびとびに並んでいる数であることが判明し、
その隙間を埋めるべく、 有理数を含む無理数という概念ができた。
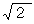 であるが、
であるが、これが分数では表すことのできない無限小数であることが証明され、
有理数は数直線上にとびとびに並んでいる数であることが判明し、
その隙間を埋めるべく、 有理数を含む無理数という概念ができた。
しかし、 無理数の集合は 「 ある数を入力すると、2乗するとその数になる数を出力する演算 」 について閉じていない。
そこで、 無理数は複素数に含まれるとし、 数の世界は複素数まで拡張された。
数の集合は、 直線から平面になったのだ。
複素数の集合は 「 ある数を入力すると、 2乗するとその数になる数を出力する演算 」 についても閉じている。
そこで、 無理数は複素数に含まれるとし、 数の世界は複素数まで拡張された。
数の集合は、 直線から平面になったのだ。
複素数の集合は 「 ある数を入力すると、 2乗するとその数になる数を出力する演算 」 についても閉じている。
 数理論 へ戻る
数理論 へ戻る