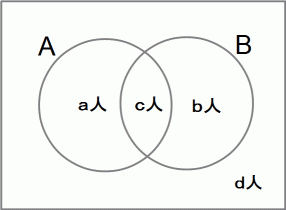
論理学 へ戻るある調査をしたところ、 犬を飼っている人はちょうど ３分の１ で、 猫を飼っている人はちょうど ４分の１ で、 犬も猫も飼っていない人が14人でした。 では、 犬も猫も飼っている人は何人だったのでしょうか？
調査対象者数は ３と４の公倍数（ 公倍数は最小公倍数の倍数 ）になっているはずです。 そこで調査対象者数が24人の場合を考えてみましょう。 この場合、 犬を飼っている人が８人、 猫を飼っている人が６人になります。 この２つをうまく部分的に重ねて合計を 10 にすることができればいいのですが、 そうです、 犬も猫も飼っている人が ４人 の場合にそうなります。（ ４ ＋（ ４ ）＋ ２ ） ＝ 10 です。
別の集団を対象に調査したところ、 犬を飼っている人はちょうど ３分の１ で、 猫を飼っている人はちょうど ４分の１ で、 犬も猫も飼っていない人が140人でした。 では、 犬も猫も飼っている人は何人だったのでしょうか？
答えは簡単で、40人 ですね。 しかし、 実際はその半分の 20人 だったそうです。 なぜでしょうか？ その答えは、 次のプログラムを実行すれば解ります。
- 全体集合を1000人以下の人とします。