【 問 題 1 】
-
全体集合を自然数とする。( 0 は含まない )
「 a と b が互いに素であるならば、
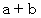 と
と 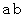 は互いに素である。」という命題が真であることを証明せよ。
は互いに素である。」という命題が真であることを証明せよ。-
この命題を「 包含命題形式 」に変換すると、 次のようになります。
「 a と b のペア が 最大公約数が 1 であるペアで構成される集合の要素 であるならば、
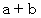 と
と 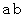 のペア も 同じ集合の要素 である。」
のペア も 同じ集合の要素 である。」この包含命題の前提命題 :
「 a と b のペア は 最大公約数が 1 であるペアで構成される集合 に属する。」
この包含命題の結論命題 :
「
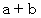 と
と 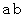 のペア は 最大公約数が 1 であるペアで構成される集合 に属する。」
のペア は 最大公約数が 1 であるペアで構成される集合 に属する。」これから背理法を用いて証明していきます。 まず、 結論命題の否定 を 結論命題 に置き換えた命題が真であると仮定します。 つまり、
「 a と b は互いに素であるならば、
 と
と 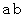 は互いに素でない。」という命題が真であると仮定します。
は互いに素でない。」という命題が真であると仮定します。すると、 結論命題の否定より、 次の式たちが成り立ちます。
a + b = kα ・ ・ ・

ab = kβ ・ ・ ・

ただし、 k > 1 α と β は互いに素
a と b は互いに素ですので、
 より、 a と b のうちどちらか1つだけが k の倍数になります。
より、 a と b のうちどちらか1つだけが k の倍数になります。a が k の倍数である場合、 次の式が成り立ちます。
a = kn ・ ・ ・

 を
を  に代入すると、
に代入すると、b = k ( α−n )
この式より、 b は k の倍数になります。 ということは、 a と b は互いに素であるという前提命題に矛盾することになります。
b が k の倍数である場合も同様にして、 a と b は互いに素であるという前提命題に矛盾することになります。
したがって、 最初の仮定が間違っていたことになります。
こうして、「 a と b が互いに素であるならば、
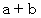 と
と 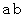 は互いに素である。」という命題が真であることが証明されました。
は互いに素である。」という命題が真であることが証明されました。-
全体集合を自然数とする。( 0 は含まない )
a と b が互いに素ならば、a と b と a+b と a×b は互いに素であることを証明せよ。
-
(1) a と a+b が互いに素であることの証明
-
a と a+b は互いに素ではないと仮定する。
すると、 a = pn a+b = pm と置くことができる。 ただし、p>1 n<m n と m は互いに素
すると、2つの式より、 b = p(m−n)
すると、a と b は互いに素ではないことになる。これは矛盾だ。
よって、a と a+b は互いに素である。
b と a+b が互いに素であることの証明も同様にしてできる。
-
a と a×b は互いに素ではないと仮定する。
すると、 a = pn a×b = pm と置くことができる。 ただし、p>1 n<m n と m は互いに素
すると、2つの式より、 b = m/n
すると、b は自然数ではないことになる。これは矛盾だ。
よって、a と a×b は互いに素である。
b と a×b が互いに素であることの証明も同様にしてできる。
-
a+b と a×b は互いに素ではないと仮定する。
すると、 a+b = pn a×b = pm と置くことができる。 ただし、p > 1 n と m は互いに素
a×b = pm より、 a または b は p の倍数である。
a が p の倍数であると仮定すると、 a = pk ( k < n ) と置くことができる。
これを a+b = pn に代入して、 b = p(n−k)
すると、b と a+b は互いに素ではないことになる。(1)より、これは矛盾だ。
b が p の倍数であると仮定しても同様の矛盾が生じる。
よって、a+b と a×b は互いに素である。
-
2つの自然数の和が 136 で、 最小公倍数が 255 のとき、 この2つの数を求めよ。
全体集合を自然数とする。( 0 は含まない )
2つの数を x,y とする。
x < y とする。
x と y の最大公約数 を Z とする。
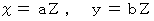 とする。
とする。a と b は互いに素である。
よって、
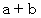 と
と 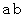 は互いに素である。 ・ ・ ・ ・
は互いに素である。 ・ ・ ・ ・ 
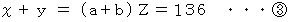
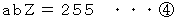
 、
、  、
、  より Z は 136 と 255 の最大公約数である。
より Z は 136 と 255 の最大公約数である。ユークリッドの互除法 :
255 ÷ 136 = 1 余り 119
136 ÷ 119 = 1 余り 17
119 ÷ 17 = 7 余り 0
したがって、
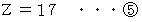
 を
を  に代入して、
に代入して、 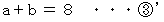
 を
を  に代入して、
に代入して、 
 と
と  より、
より、 
したがって、 2つの数は、 51 と 85 である。
 数理論 へ戻る
数理論 へ戻る