オイラーの多面体定理:
任意の凸多面体について次の式が成り立つ:
( 頂点の数 )-( 辺の数 )+( 面の数 )= 2
( 頂点の数 )-( 辺の数 )+( 面の数 )= 2
内腔を持つ閉じた立方体についてのオイラーの多面体定理の式:
( 頂点の数 )-( 辺の数 )+( 面の数 )= 8 - 12 + 6 = 2 ・・・ ①
【 証 明 】
-
内腔を持つ閉じた立方体の天井の面のみを除去すると、
頂点 と 辺 は1つも除去されないので、①の式は次のように変化する。
8 - 12 + 5 = 1 ・・・ ②
次の図は、それを真上からのぞき込んだ図で、立方体の内面を見た図になる。真中の正方形は立方体の底面の内側になる。辺は赤色で表している。
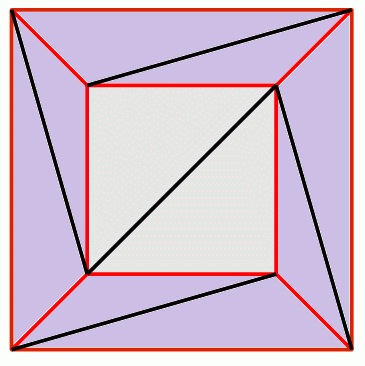
なお、それぞれの面の内側に対角線を1本ずつ黒線で引いて、正方形を2つの三角形に分割している。したがって、辺と面が5つずつ増えているので、②の式は次のように変化している。
8 - 17 + 10 = 1 ・・・ ③
これから三角形を4枚除去すると、次のようになる。
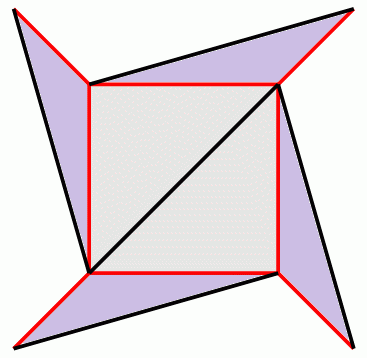
除去した三角形1枚につき辺と面が1つずつ消失するので、③の式は次のように変化する。
8 - 13 + 6 = 1 ・・・ ④
さらに三角形を4枚除去すると、次のようになる。
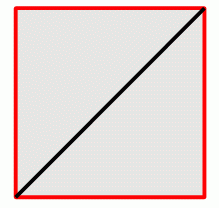
除去した三角形1枚につき頂点と面が1つずつ辺が2つ消失するので、④の式は次のように変化する。
4 - 5 + 2 = 1 ・・・ ⑤
さらに三角形を1枚除去すると、次のようになる。
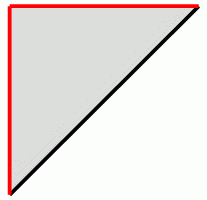
除去した三角形1枚につき頂点と面が1つずつ辺が2つ消失するので、⑤の式は次のように変化する。
3 - 3 + 1 = 1 ・・・ ⑥
② から ⑥ の式の右辺はすべて1であることに注目していただきたい。
では、 ② から ⑥ の式を順番を反対にして並べてみよう。
3 - 3 + 1 = 1
↓
4 - 5 + 2 = 1
↓
8 - 13 + 6 = 1
↓
8 - 17 + 10 = 1
↓
8 - 12 + 5 = 1
上記の式の変化は何を表しているのかというと、最初に1つの三角形があり、その三角形の辺に新たな三角形の辺を貼り合わせて図形をどんどん広げていったとき、それは平面から空間の図形へと拡張していくが、内腔を持つ閉じた多面体にならない限りは、次の式の関係が保たれるということを表している。
( 頂点の数 )-( 辺の数 )+( 面の数 )= 1
したがって、最後に1枚の面を貼り付けて内腔を持つ閉じた多面体が完成したときには、面の数のみが1つ増えるので、次の式が成り立つ。
( 頂点の数 )-( 辺の数 )+( 面の数 )= 2
これが、オイラーの多面体定理である。
 幾何学 へ戻る
幾何学 へ戻る