タレスの定理： 直径に対する円周角は直角である。

　　　　　　　


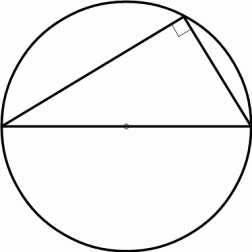
【 証 明 その１ 】

　　　　

　 円の中心 と 円周角を作る円周上の点 とを線分で結ぶ。 すると、 ２つの二等辺三角形ができる。 上図のように角度を ａ ，ｂ とすると、 次の式が成り立つ。
　　　　( ａ＋ｂ ) ＋ ａ ＋ ｂ　＝　180
　　　　　　　　　または、
　　　　（ 180 − 2ａ ） ＋ （ 180 − 2ｂ ）　＝　180

　　　　よって、 ａ ＋ ｂ　＝　90

【 証 明 その２ 】

∠A ＝ 90° の直角三角形ABCを作り、辺BCを x 座標軸上に乗せ、辺BCの中点を原点に持ってくる。
A ( x, y )　　B (−b, 0 )　　C ( b, 0 )　　∠ACB ＝ θ　とする。

　　sin²θ ＝ { ( x＋b ) ²＋ y² } ÷ 4b²
　　cos²θ ＝ { ( x−b ) ²＋ y² } ÷ 4b²

　　sin²θ ＋ cos²θ ＝ ( x²＋y²＋b² ) ÷ 2b² ＝ 1
よって、
　　x²＋y²＋b² ＝ 2b²
よって、
　　x²＋y² ＝ b²
この式より、点Ａは半径 b の円の円周上にあることが分かる。