【 問 題 １ 】

　サイコロを n 回振ったら、出た目の数の和が n+3 になった。何通りのパターンがあるか？

【 解 答 】

　すべて 1 が出たとしたら、出た目の数の和が n+3 よりも 3 だけ少ないことになるから、どこかで合計3 だけ多く出ていなければならない。ということは、3 を 0 と 1 と 2 と 3 の数のどれかの数の合計 n 個の数の和で表す全ての場合の数を求めればいいことになる。


【 方法その１ 】
n=1 のとき、3 だけの 1 通り
n=2 のとき、0+3, 3+0, 1+2, 2+1 の 4 通り
n=3 のとき、
　　3 と 0 だけの場合の数 : n 通り
　　1 と 0 だけの場合の数 : _nＣ₃ 通り
　　2 と 1 と 0 だけの場合の数 : _nＣ₃ 通り
　　したがって、
　　　　 n ＋ _nＣ₃ ＋ 2×_nＣ₂
　　　　　　　　　　　
　　　　　　　　　　　
　　　　　　　　　　　
　　　　　　　　　　　
　　　　　　　　　　　

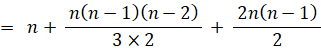
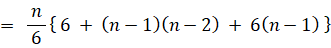
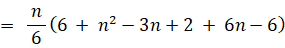
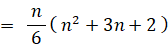
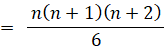
n=1 のとき、
　　　
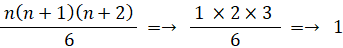
n=2 のとき、
　　　
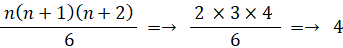
よって、すべての n について次の式が成り立ち、答えは次の式になる。
　　　　　　　　　　　



【 方法その２ 】
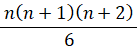
３個の 1 と n−1 個の楔(くさび)を一列に並べる場合の数と同じである。
それは n＋2 個の席から３つの組み合わせを選ぶのと同じだから、
　　　_n＋2Ｃ₃
　　　　　　

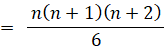
※ 参照： 確率 ＞ 分け合う場合の数