【 問 題 】

ボタンを押すと １ 〜 ４ までの自然数のうちの１つを表示する器械がある。
数ごとの表示される確率は次のようになっている。
　　１： 0.1　　　２： 0.2　　　３： 0.3　　　４： 0.4
２回ボタンを押して表示される数の和をとるとき、その期待値を求めよ。

【 解 答 】

	１	２	３	４
１	0.01	0.02	0.03	0.04
２	0.02	0.04	0.06	0.08
３	0.03	0.06	0.09	0.12
４	0.04	0.08	0.12	0.16


2 :　0.01
3 :　0.02 ＋ 0.02　＝→　0.04
4 :　0.03 ＋ 0.04 ＋ 0.03　＝→　0.1
5 :　0.04 ＋ 0.06 ＋ 0.06 ＋ 0.04　＝→　0.2
6 :　0.08 ＋ 0.09 ＋ 0.08　＝→　0.25
7 :　0.12 ＋ 0.12　＝→　0.24
8 :　0.16

0.01 ＋ 0.04 ＋ 0.1 ＋ 0.2 ＋ 0.25 ＋ 0.24 ＋ 0.16　＝→　１
2×0.01 + 3×0.04 + 4×0.1 + 5×0.2 + 6×0.25 + 7×0.24 + 8×0.16　＝→　６

答えは ６ です。

【 別 解 】

( 0.1 x ¹ ＋ 0.2 x ² ＋ 0.3 x ³ ＋ 0.4 x ⁴ ) ²
　　　＝　0.01 x ² ＋ 0.02 x ³ ＋ 0.03 x ⁴ ＋ 0.04 x ⁵
　　　　　　 　　＋ 0.02 x ³ ＋ 0.04 x ⁴ ＋ 0.06 x ⁵ ＋ 0.08 x ⁶
　　　　　　　　　　　　　＋ 0.03 x ⁴ ＋ 0.06 x ⁵ ＋ 0.09 x ⁶ ＋ 0.12 x ⁷
　　　　　　　　　　　　　　　　　1＋ 0.04 x ⁵ ＋ 0.08 x ⁶ ＋ 0.12 x ⁷ ＋ 0.16 x ⁸
　　　＝　0.01 x ² ＋ 0.04 x ³ ＋ 0.1 x ⁴ ＋ 0.2 x ⁵ ＋ 0.25 x ⁶ ＋ 0.24 x ⁷ ＋ 0.16 x ⁸

0.01 ＋ 0.04 ＋ 0.1 ＋ 0.2 ＋ 0.25 ＋ 0.24 ＋ 0.16　＝→　１
2×0.01 + 3×0.04 + 4×0.1 + 5×0.2 + 6×0.25 + 7×0.24 + 8×0.16　＝→　６

答えは ６ です。

　　　　　※ 参照：　大学生のための数学 ＞ その他の数学 ＞ 畳み込み演算（ 離散的 ）



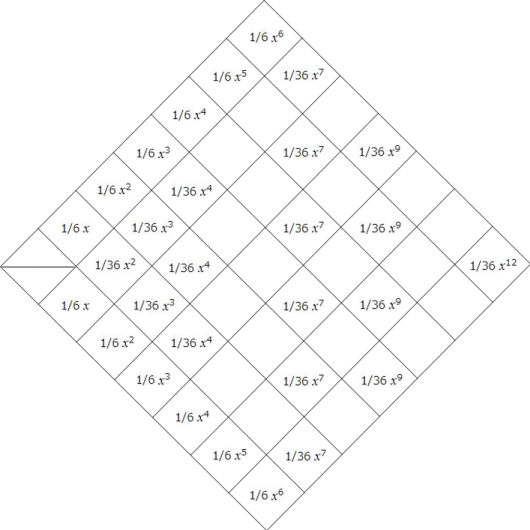
　サイコロを２回振ったときの出た目の合計の確率分布を求めてみましょう。確率変数は２以上12以下の自然数で非連続です。確率変数を横軸に確率を縦軸に取ってグラフで表すと、それは、棒グラフになり、棒の高さの総和が１になります。

　その棒グラフの横軸の値や縦軸の値は次の方程式より導くことができます。左辺の x の累乗数はサイコロを１回振ったときに出る目の数を表し、係数 1/6 はその目が出る確率を表し、右辺の x の累乗数はサイコロを２回振ったときの出た目の合計を表し、右辺の係数は出た目の合計が累乗数になる確率を表しています。

　　　( 1/6 x ＋ 1/6 x² ＋ 1/6 x³ ＋ 1/6 x⁴ ＋ 1/6 x⁵ ＋ 1/6 x⁶ ) ²
　　　　　　　　　　　＝　1/36 x² ＋ 2/36 x³ ＋ 3/36 x⁴ ＋ 4/36 x⁵ ＋ 5/36 x⁶ ＋ 6/36 x⁷
　　　　　　　　　　　　　　　　　　　＋ 5/36 x⁸ ＋ 4/36 x⁹ ＋ 3/36 x¹⁰ ＋ 2/36 x¹¹ ＋ 1/36 x¹²