(1) 漸化式の線形性
-
以下の漸化式で与えられる2つの数列があります。
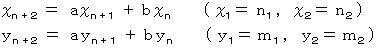
2つの漸化式より、 次の式が成り立ちます。
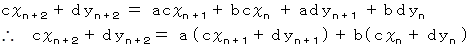
したがって、
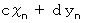 も同じ漸化式で与えられる数列であることが解ります。
も同じ漸化式で与えられる数列であることが解ります。たとえば、
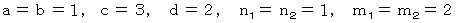 のとき、
のとき、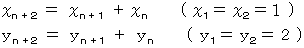

これから、 その理由を考えてみましょう。
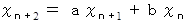 の形の漸化式で表される数列が、 初項 1 、 公比 r の等比数列であると仮定すると、 次のように書くことができます。
の形の漸化式で表される数列が、 初項 1 、 公比 r の等比数列であると仮定すると、 次のように書くことができます。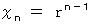
これを
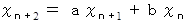 に代入すると、
に代入すると、
したがって、
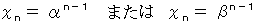
(1) の線形性より、
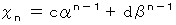
では 、練習問題を解いてみましょう。
-
問題 : 次の漸化式で与えられる数列の第 n 項を求めよ。
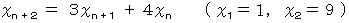
解答 :
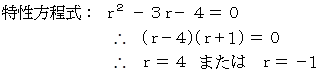
したがって、
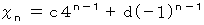
ここで、
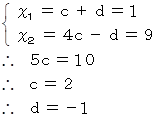
したがって、
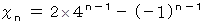
以上が答えである。 この数列は次のようなものである。
1 9 31 129 ・ ・ ・ ・
【 別 解 】
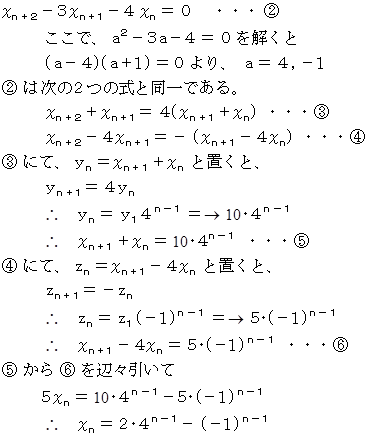
 数理論 へ戻る
数理論 へ戻る