数理論 へ戻る１ から
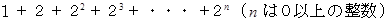までの整数は、 必ず 
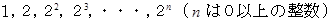の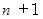 
個の数を足したり引いたりして作ることができます。１ から
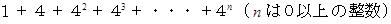までの整数は、 必ずしも 
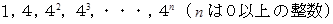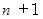の 個の数を足したり引いたりして作ることはできません。以上のことを、 次の十進BASIC のプログラムを実行して確かめてみましょう。
１ から
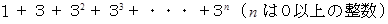までの整数は、 必ず 
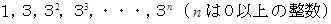の 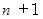個の数を足したり引いたりして作ることができます。このことは、 次の十進BASIC のプログラムたちを実行すると解ります。
【 問 題 １ 】
-
200ｇの砂糖があります。 上皿天秤 と １ｇ、２ｇ、４ｇ、８ｇ、16ｇ、32ｇ、64ｇ の重りが１個ずつあれば、 上皿天秤の片方の皿にのみ重りを載せて、 １回の測定だけで １ｇ から 199ｇ まで１ｇ単位で任意の量の砂糖を量り出せることを示してください。
-
100ｇまで測り出すことができれば、 それ以上の量を量り出すことは可能です。 残った方がその量になっているからです。 また、 重りの総質量は100ｇを超えているので大丈夫です。
重りの数列が
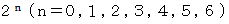で表されることに注目してください。 したがって、 この問題は、 すべての100以下の自然数 ｎ を次のような形式に展開できることを証明する問題と同じです。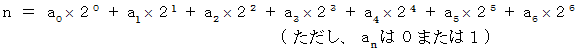
上の式は１０進数を２進数に変換する式であり、 これを 「 ２進法展開 」 と言うことにしましょう。 すべての10進数の数を２進法展することができることは明らかです。
【 問 題 ２ 】
-
200ｇの砂糖があります。 上皿天秤 と １ｇ、３ｇ、９ｇ、27ｇ、81ｇ の重りが１個ずつあります。 １回の測定だけで １ｇ から 199ｇ まで１ｇ単位で任意の量の砂糖を測り出せることを示してください。 なお、 重りはどちらの皿に乗せても結構です。
-
100ｇまで測り出すことができれば、 それ以上の量を測り出すことは可能です。 残った方がその量になっているからです。 また、 重りの総質量は100ｇを超えているので大丈夫です。
重りの数列が
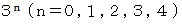で表されることに注目してください。 したがって、 この問題は、 すべての100以下の自然数 ｎ を次のような形式に展開できることを証明する問題と同じです。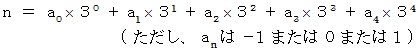
これを 「 平衡３進法展開 」 と言うことにしましょう。
|
10進法 |
３進法 |
平衡３進法 |
|
0 0 0 |
0 0 0 |
0 0 0 |
|
0 0 1 |
0 0 1 |
0 0 1 |
|
0 0 2 |
0 0 2 |
0 1-1 |
|
0 0 3 |
0 1 0 |
0 1 0 |
|
0 0 4 |
0 1 1 |
0 1 1 |
|
0 0 5 |
0 1 2 |
1-1-1 |
|
0 0 6 |
0 2 0 |
1-1 0 |
|
0 0 7 |
0 2 1 |
1-1 1 |
|
0 0 8 |
0 2 2 |
1 0-1 |
|
0 0 9 |
1 0 0 |
1 0 0 |
平衡３進法展開を用いて、 意図した砂糖の量を量り出す方法を求めるプログラムを作ることができます。 十進BASIC のプログラムを下枠の中に示します。
-
JavaScript のプログラム:
プログラムの内容 ：