全体集合を ０ 以上 １ 以下の有理数とします。
１ 段目の分数の数列を次に示します。
　　　　
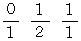
　 小さい順に並んでいます。 両端の分数は本当は整数です。 端ではない分数は既約分数 （ これ以上 約分できない分数 ） です。
　 １ 段目の隣どうしの分数の分母どうしを加えたものを分母とし分子どうしを加えたものを分子とする新たな分数を作り、 その間に配置します。 同じ操作をすべての隣どうしの分数のペアに対して行いそれを２段目とします。 したがって２段目は次のようになります。
　　　　
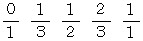
同様にして、 ３段目は次のようになります。
　　　　
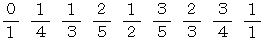
同様にして、 ４段目は次のようになります。
　　　　
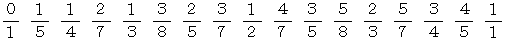
小さい順に並んでいます。 端ではない分数は既約分数です。

さて、 ｎ 段目は何個の分数の数列になるでしょうか？
ｎ 段目の分数の個数 を 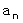とします。
　　　　

　 ここで、１段目から４段目までの分数の数列に再び注目してください。 隣どうしの分数の分母と分子を交差するように掛け合わせたものの差を取ってください。 例えば a/b と c/d ならば ｜ bc − ad ｜ になります。 どうですか？　すべて １ になっていますね。
　 b ＞ d　のとき、 ｜ bc − ad ｜ ＝ １ ならば、「 分母が b 以下の既約分数において、 a/b と c/d は 隣り合う既約分数である。」と言うことにします。
　 こういった大きさの点で隣り合う既約分数の性質を発見したのはファレイという人で、 「 ファレイ数列 」 というのがあります。 たとえば「 ５に属するファレイ数列 は次のようなものです。
　　　　

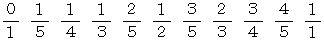
〇に属するファレイ数列を表示する 十進BASIC のプログラム ：