その他の数学 へ戻る２次元 x y 平面座標系があります。一辺の長さが２の正方形ＡＢＣＤがあり、その重心Ｐの位置ベクトルは（ x, y ）＝（ 0, 3 ）で表されます。
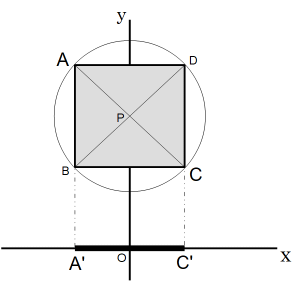
正方形ＡＢＣＤを重心Ｐを中心として反時計回りに 90度回転させるとき、正方形ＡＢＣＤの x 軸上への投影像は、直線ＡＣを重心Ｐを中心として反時計回りに 90度回転させるときの x 軸上への投影像Ａ'Ｃ' と等しくなります。このとき、Ａ'Ｃ' の平均長がいくらになるか考えて見ましょう。
-
正方形ＡＢＣＤの回転角度を θ (rad) とすると、θ は一定の大きさで増大していきます。
ＰＣ ＝ root(2)
ＰＣ と x 軸 とのなす角 は、 π/4−θ (rad) です。
したがって、次の式が成り立ちます。
Ａ'Ｃ' ＝ 2 × root(2) × cos(π/4−θ)
よって、Ａ'Ｃ' の平均長は次の式で与えられます。
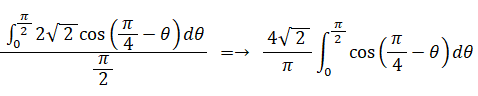
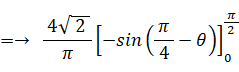
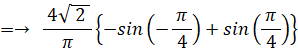
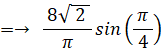
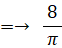
≒→ 2.546
ちなみにＡ'Ｃ' の最大幅はおよそ 2.828 です。
＜ JavaScript シミュレーション プログラム ＞