固有空間とは、固有ベクトル と ゼロベクトル とからなる集合のことです。
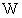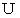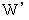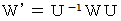　 演算テンソル の 「 固有テンソル 」 （ 私の造語です ） を とすると、 固有空間へ座標変換された演算テンソル は で表され、 その表現行列は 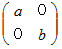の形で表されます。

さて、 次の式が成り立ちます。
　　　

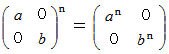
また、 次の式も成り立ちます。
　　　
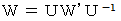
　 以上の３つのことから、 演算テンソル 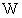の表現行列を 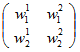とするとき、 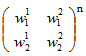を求めるために、 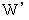の表現行列のｎ乗を求めてから、 それを元のベクトル空間に座標変換してやるという方法をとれば、 容易に求めることができることが解ります。

　 以上のアルゴリズムを使って行列のｎ乗を求めるプログラムを十進BASIC で作ってみました。

　 他の方法で行列の ｎ 乗を求めることもできます。
そのためには、　線形代数学 ＞ 正方行列の ｎ 乗　をご覧ください。