(1) スペクトル分解を利用する方法
-
次のような行列A がある。 Aのn乗を求めてみよう。
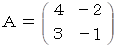
まず、 行列A を表現行列とする演算テンソルの代表的固有ベクトルを2つ求める。
固有値を λ とすると、
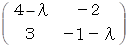 の行列式が 0 になるので、 次の式が成り立つ。
の行列式が 0 になるので、 次の式が成り立つ。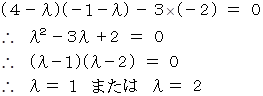
これで2つの固有値が見つかった。
ここで、 P + Q = E と 2P+1Q = A( 2と1はAの固有値 ) とを満たす 2つの要列 P と Q を見つける。
P + Q = E と 2P+1Q = A を連立させて解くと、
Q = 2E−A P = −E+A
よって、
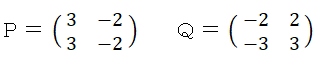
※ 参照: 線形代数学 > 固有値に関する行列の性質
すると、 次の5つの式が成り立つ。
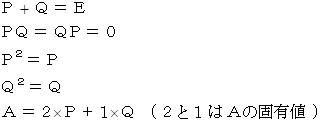
※ 参照: 線形代数学 > 射影行列とは
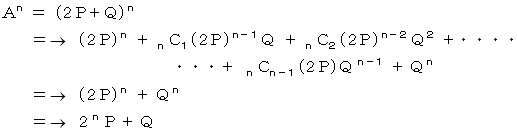

以上が答えである。 たとえば、n=2 のとき、
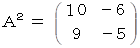
十進BASIC > 十進BASIC_行列 > 行列のn乗
(3) 行列の対角化による方法 ( お勧めです )
線形代数学 > 固有空間の利用法の1つ
-
次のような行列A がある。 Aのn乗を求めてみよう。
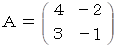
まず、 行列A を表現行列とする演算テンソルの代表的固有ベクトルを2つ求める。
固有値を λ とすると、
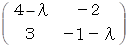 の行列式が 0 になるので、 次の式が成り立つ。
の行列式が 0 になるので、 次の式が成り立つ。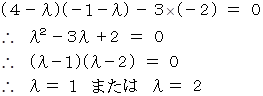
これで2つの固有値が見つかった。
λ = 1 のとき、
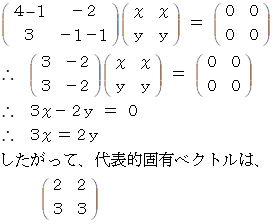
λ = 2 のとき、
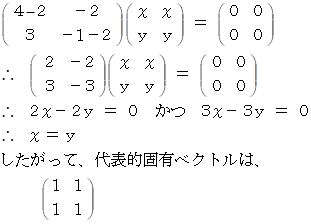
そこで、 固有空間に座標変換するテンソルは
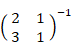 となり、次の式が成り立つ。
となり、次の式が成り立つ。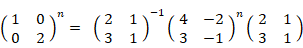
したがって、
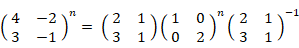
ここで、
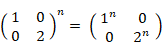
したがって、
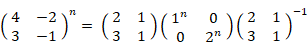
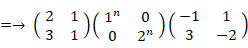
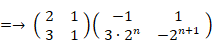
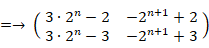
 線形代数学 へ戻る
線形代数学 へ戻る