【 問 題 】

最長の辺の長さが等しい直角三角形のうち面積が最大のものは直角二等辺三角形であることを証明せよ。

【 解 答 １ 】

　直角になっている頂点から最長の辺までの距離に最長の辺の長さをかけて2で割ると直角三角形の面積になる。

　直角三角形の最長の辺の長さに等しい直径を持つ円の直径を直角三角形の最長の辺とし、その円の円周上の点を直角になっている頂点として、その点を円周上で移動させると、最長の辺の長さが等しい全ての直角三角形ができる。

　このとき、直角になっている頂点から最長の辺までの距離が最大になるのは、直角二等辺三角形になるときであり、そのときの値は円の半径、つまり、最長の辺の長さの半分に等しくなっている。

　　　　　　

【 解 答 ２ 】

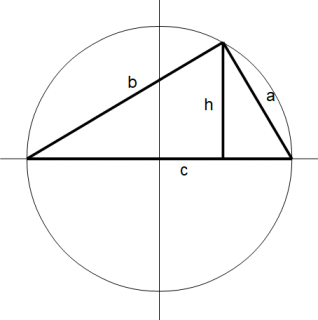
　直角二等辺三角形の底辺を最長の辺とすると、直角三角形の高さは最長の辺の長さの半分になる。直角三角形の最長の辺の長さを c とし、直角三角形の高さを h とする。また、直角三角形の他の辺の長さを a と b（ a ≦ b ）とする。すると、
　　　a² ＋ b² ＝ c²
　　　２つの三角形が相似であることより、 h：a ＝ b：c　→　h ＝ ab/c

　h ＞ c/2 と仮定すると、
　　　ab/c ＞ c/2
　　　よって、 2ab ＞ c²
　　　よって、 2ab ＞ a² ＋ b²
　　　よって、 ０ ＞ ( a − b )²
上記の式は明らかに間違いである。
したがって、 h ≦ c/2 であることが分かる。

　h ＝ c/2 のとき、
　　　c/2 ＝ ab/c
　　　よって、 c² ＝ 2ab
　　　よって、 a² ＋ b² ＝ 2ab
　　　よって、 ( a − b )² ＝ ０
　　　よって、 a ＝ b

　したがって、 最長の辺の長さが等しい直角三角形のうち高さが最高になるのは直角二等辺三角形であることが分かった。最長の辺の長さが等しい直角三角形のうち高さが最高のものは、面積も最大になるで、最長の辺の長さが等しい直角三角形のうち面積が最大のものは直角二等辺三角形であることが分かる。