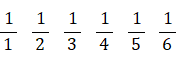
上記の数列は次の漸化式で与えられます。
　　　
　　　　　　　　　

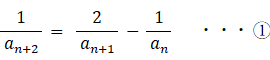
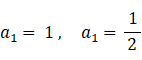
a₃ を求めましょう。
　　　
　　　　　
　　　
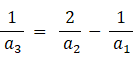
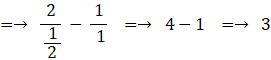
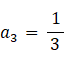
a₄ を求めましょう。
　　　
　　　　　
　　　
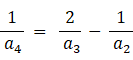
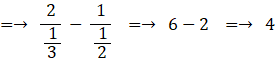
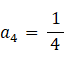
�@ は次のように変形されます。
　　　

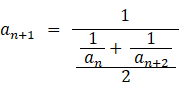
　これを見ると、ある項の値は前後の項の調和平均（ 逆数の平均の逆数 ）になっています。ですから、自然数の逆数の数列は調和数列（ 各項の逆数が等差数列になる数列 ）に属します。
　　　　　　　※ 参考： ばいおりんの日常的物理学文集 ＞ 音楽と数学 ＞ 調和の弦奏

　自然数の逆数の数列の和は発散します。その理由は別の論文 数理論 ＞ 平方数の数列の和（ バーゼル問題を含む ）の（２）をご覧ください。