思考実験につき空気抵抗はないものとします。
両端が壁で完全に固定された摩擦の生じないテーブルがあります。
テーブルの上の中央で静止している質量 1 kg の立方体Ａがあります。
テーブルの左側から質量 1 kg の立方体Ｂが速さ 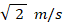の等速直線運動をしてきて、立方体Ａに完全弾性衝突をしました。
その後、立方体Ｂは静止したままで、立方体Ａは右方向に速さ 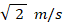の等速直線運動をして壁と完全弾性衝突をします。
すると、立方体Ａの運動は瞬時に左方向への速さ 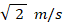の等速直線運動に変わります。
その後、立方体Ａは立方体Ｂに完全弾性衝突をします。
すると、その後、立方体Ａは静止したままで、立方体Ｂは左方向に速さ 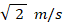の等速直線運動をして壁と完全弾性衝突をします。
すると、立方体Ｂの運動は瞬時に右方向への速さ 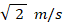の等速直線運動に変わります。
その後、立方体Ｂは立方体Ａに完全弾性衝突をします。
以上の一連の運動が永遠に繰り返されます。

立方体Ａの速さを v₁ とし、立方体Ｂの速さを v₂ とし、質量を m₁ ＝ m₂ ＝ 1 とします。

運動エネルギー保存の法則：
　　　
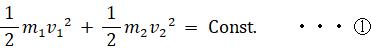
運動量保存の法則：
　　　

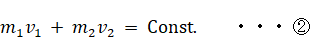
次のように置きます。
　　　　　　
すると、�@ より、
　　　
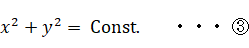
�A より、
　　　

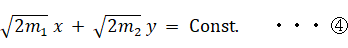
m₁ ＝ m₂ ＝ 1 より、�C は次のようになります。
　　　
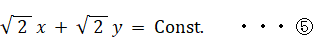
初期条件 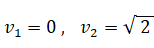より、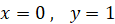 になります。したがって、
�B は次のようになります。
　　　
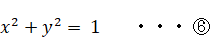
�D は次のようになります。
　　　
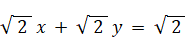
　よって、
　　　

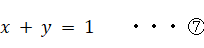
立方体Ａが壁と完全弾性衝突をした直後から �F は次のように変わります。
　　　x ＋ y ＝ −1　　・・・ �G
この式は、その後に、立方体Ｂが壁と完全弾性衝突をした直後から �F に再び変化します。

�E �F �G のグラフを書くと次のようになります。交点をそれぞれ Ａ,Ｂ,Ｃ,Ｄ とします。
　　　

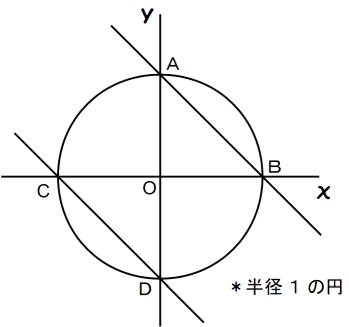
初期条件：しばらく点Ａの位置に留まる　→　立方体Ｂが立方体Ａに衝突 ＝ 点Ｂの位置へジャンプ
　　　　→ しばらく点Ｂの位置に留まる　→　立方体Ａが壁に衝突 ＝ 点Ｃの位置へジャンプ
　　　　→ しばらく点Ｃの位置に留まる　→　立方体Ａが立方体Ｂに衝突 ＝ 点Ｄの位置へジャンプ
　　　　→ しばらく点Ｄの位置に留まる　→　立方体Ｂが壁に衝突 ＝ 点Ａの位置へジャンプ
　　　　→ しばらく点Ａの位置に留まる　→　立方体Ｂが立方体Ａに衝突 ＝ 点Ｂの位置へジャンプ
　　　　→ しばらく点Ｂの位置に留まる　→　（ 省 略 ）
つまり、 Ａ→Ｂ→Ｃ→Ｄ→Ａ→Ｂ→Ｃ→Ｄ→Ａ→ ・・・・