「 回転を伴わない移動（ 平行移動 ）をして、 ベクトルの頭にベクトルのお尻をくっつけたら、 ベクトルのお尻から頭までを結んで出来あがり。」というのが、ベクトルのたし算です。 ベクトルの頭とはベクトルの終点のことで、 ベクトルのお尻とはベクトルの起点のことです。 ベクトルのひき算は、ひく方のベクトルの逆ベクトルを足すのと同じです。

　 ではベクトルのかけ算は？ 「 ベクトルのかけ算には内積と外積の２種類があります。」と言いたいのですが、 内積の結果はベクトルではないスカラーになり、 外積の結果は２次元平面ではない３次元空間になりますので、 これらはベクトルのかけ算ではありません。

　 ベクトルのかけ算はあります。 それは次のようなものです。

　　　　　　

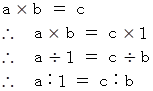
ａ の １ に対する在り方 と ｃ の ｂ に対する在り方 とは、 等しい。
　　　　　　　　　　 　　　　　↓↓
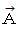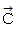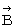の 基底ベクトル に対する在り方 と の に対する在り方 とは、 等しい。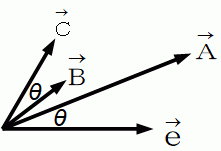

　　　　　

　 したがって、 上図のように、 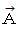× 　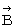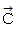＝　　は 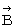を 反時計回りに θ 回転して、 大きさを 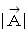倍したものです。
　　　　　　　　　　　　　※　ここでは、 演算子 × は外積を表わす記号ではありません。

追伸 ：

　ベクトルのたし算とかけ算の座標表示については、 次の式を参考にしてください。
　　　　　
　　　　　

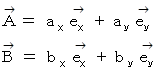
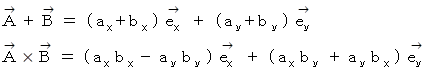
　 大学生のための数学 ＞ 数理論 ＞ 物理学における複素数の意味 も ベクトルのかけ算 に関連する論文です。