今回は「 ベクトル類似度 」の提案をさせていただきます。

　 最初に２つのベクトルが作る角度の表現方法について、 次のような約束をさせていただきたいと存じます。
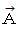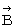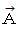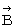　ベクトル を反時計回りにθラジアン回転させると と同じ向きになるとき、 に対する の角度は θラジアン（ −２π ≦ θ ≦ ２π ）であると言うことにします。

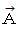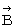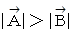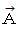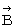　 ２つのベクトル と とがあります。 であり、 かつ、 に対する の角度は θラジアンであるとします。 このとき、 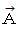と 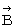との「 ベクトル類似度 」の定義を次のようにすることにします。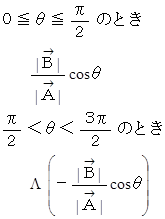

　　　　　　

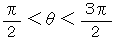　 のとき、 記号 は２つのベクトルが比較的に反対向きになっていることを表します。 またその後に続く値は正の数になります。

　「 ベクトル類似度 」が １ であるということは、 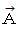と とは同じベクトルであるということを意味します。 今からその理由を述べます。

　 定義より、「 ベクトル類似度 」が １ であるための必要条件は、 ２つのベクトルの作る角度が90度以下であるということです。 次に、
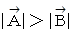　　　　　　 　なので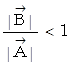　
　　　　　　また、　cosθ ≦ １
　　　　　　よって、
　　　　　　　　　　

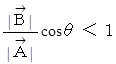
　 以上より、 ２つのベクトルの大きさが異なるときには決してベクトル類似度は １ にならないことがわかります。 最後に 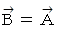として定義式に当てはめると １ になることが解ります。

　 最後に「 ベクトル類似度 」が 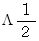になるのはどんな場合かを考えてみましょう。 まず、 ４つの場合が浮かんでくると思います。 それは、

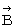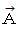　　　 が と反対向きで大きさが半分のとき
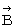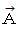　　　 が と反対向きで大きさが２倍のとき
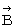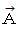　　　 が と同じ大きさで 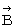に対する角度が120度のとき
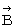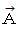　　　 が と同じ大きさで 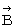に対する角度が−120度のとき

　 しかし、 それだけではありません。 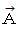と 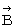とが作る角度が 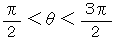で、 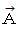の大きさが次の式で与えられるときも「 ベクトル類似度 」が 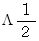になります。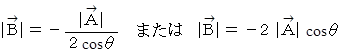
　　　　　
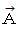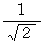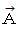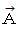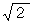　 たとえば、 の大きさの で に対する角度が 135度のベクトルや、 の大きさの で 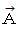に対する角度が −135度のベクトルが、 それに相当します。