半径が １ ： ２ の車輪を中心を重ねて固定し軸を付け、 同時に回転するようにします。 真っ直ぐなレールを水平に２本設置して、 ２つの車輪が同時に転がるようにします。そして、 大きな車輪が転がるレールには滑り止めを塗り、 小さな車輪が転がるレールには潤滑油を塗ります。 大きな車輪を １ 回転させると小さな車輪も １ 回転します。 大きな車輪が移動した距離は円周の長さと同じですが、 小さな車輪が移動した距離は円周の長さの２倍です。 そこで、 小さな車輪の円周の長さは大きな車輪の円周の長さに等しいのではないかという疑惑が生じます。 しかし、「 小さな車輪は滑りながら転がり、 その割合は半々であった。」と考えると辻褄が合います。

　　　　　　　　　


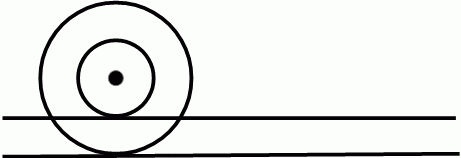
　 しかし、 これに新たな疑惑を投げかけるパラドックスが登場しました。 まず思い浮かべてください。 玉が転がっている場面と玉が滑っている場面を。 「 転がる 」 は、 物質と床の接点に関して、 物質の接点と床の接点は １ 対 １ に対応していますが、 「 滑る 」 は、 物質の接点と床の接点は １ 対 多 の対応になっています。 さて、 小さな車輪とレールとの接点に関して言えば、 それは、 小さな車輪の接点とレールの接点が １ 対 １ に対応しています。 したがって、「 小さな車輪は滑ることなく、 転がるだけである。」ということになり、「小さな車輪の円周の長さは大きな車輪の円周の長さに等しい。」という不思議な結論に戻ってしまうのです。

　「 集合Ａ の要素と集合Ｂ の要素が １ 対 １ に対応しているならば、 ２つの集合の要素の数は等しい。」という法則があります。 レールの小さな車輪との接点の最初の接点からの距離は、 小さな車輪のレールとの接点の最初の接点からの道のりの２倍になっていますが、 それまでの間、 小さな車輪の接点とレールの接点とは １ 対 １ 対応になっています。　 y ＝ ２ x 　の１ 対 １ 対応です。

　 この新しいパラドックスの正解はというと、　d y ＝ ２d x　で、 接点とすぐ隣の接点との距離がレールは小さな車輪の２倍になっているので、 小さな車輪の接点がすぐ隣の接点にとって代わられるまでに、 小さな車輪の接点は、 瞬間的に、 その接点とすぐ隣の接点との距離の２倍の距離を移動しているということになり、 その半分の距離だけ小さな車輪は滑っていると考えることができるのです。

　参考：
　　　大学生のための物理学 ＞ 剛体力学 ＞ すべり回転
　　　ばいおりんの日常的物理学文集 ＞ 数学と物理学 ＞ 微小２点間距離