【 問 題 1 】
-
n が自然数ならば、
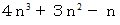 は 6で割り切れることを証明しなさい。
は 6で割り切れることを証明しなさい。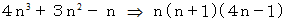
n が自然数ならば、 n または
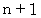 は2で割り切れる。 よって、
は2で割り切れる。 よって、 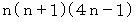 は2で割り切れる。
は2で割り切れる。k が 0 以上の整数ならば、
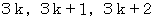 で作られる整数の集合は、 0以上の整数の集合に等しい。
で作られる整数の集合は、 0以上の整数の集合に等しい。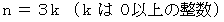 のとき、
のとき、n は 3で割り切れる。
よって、
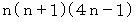 は 3で割り切れる。
は 3で割り切れる。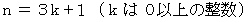 のとき、
のとき、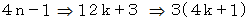 だから、
だから、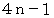 は 3で割り切れる。
は 3で割り切れる。よって、
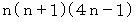 は 3で割り切れる。
は 3で割り切れる。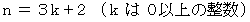 のとき、
のとき、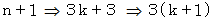 だから、
だから、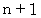 は 3で割り切れる。
は 3で割り切れる。よって、
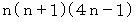 は 3で割り切れる。
は 3で割り切れる。以上より、
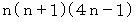 は 3で割り切れる。
は 3で割り切れる。6 = 2 × 3
是故 ( そういうわけで )、 n が自然数ならば、
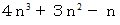 は 6で割り切れる。
は 6で割り切れる。-
全体集合を自然数とする。
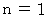 のとき、
のとき、 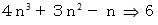 だから
だから 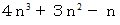 は 6で割り切れる。
は 6で割り切れる。 のとき、
のとき、 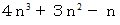 は 6で割り切れると仮定する。 つまり次の式が成り立つと仮定する。
は 6で割り切れると仮定する。 つまり次の式が成り立つと仮定する。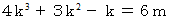
 のとき、
のとき、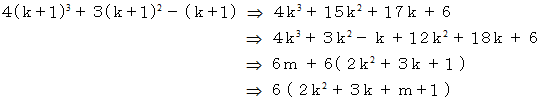
したがって、
 のとき、
のとき、 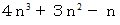 は 6で割り切れることが解る。
は 6で割り切れることが解る。よって、
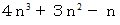 は 6で割り切れることが判った。
は 6で割り切れることが判った。-
全体集合を自然数とします。 次の3つを証明しなさい。

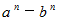 は
は 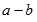 で割り切れる。
で割り切れる。
 が偶数のとき、
が偶数のとき、 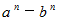 は
は 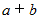 で割り切れる。
で割り切れる。
 が奇数のとき、
が奇数のとき、 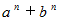 は
は 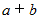 で割り切れる。
で割り切れる。 の証明 :
の証明 :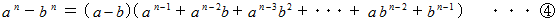
 の証明 :
の証明 : で、
で、 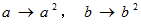 と置き変えると、
と置き変えると、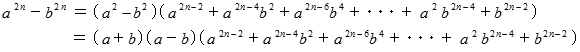
 の証明 :
の証明 : で、
で、 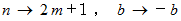 と置き変えると、
と置き変えると、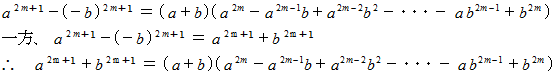
 数理論 へ戻る
数理論 へ戻る