ウィルソンの定理の証明その1:
ある自然数の階乗に1を加えた数は素数です。
なぜなら、その数は、2以上その数未満の全ての自然数で割った余りが全て1になるから。
素数の階乗はその素数で割り切れます。
なぜなら、その数は、2以上その数未満の全ての自然数で割った余りが全て1になるから。
素数の階乗はその素数で割り切れます。
↓↓ ↓↓
素数から 1 を引いた数の階乗 を その素数で割ると その余りは その素数から 1 を引いた数 になる。
( ウィルソンの定理 )
( ウィルソンの定理 )
ウィルソンの定理の証明その2:
ある素数から1を引いた数の階乗を、その素数を法とする乗法とみなすとき、2 以上 その素数から2を引いた数 以下 の偶数個の数たちは、掛け合わすと1になるペア( 逆元どうしの関係 )を漏れなく形成する。したがって、ある素数から1を引いた数の階乗をその素数で割った余りは、その素数から1を引いた数になる。
アルファベットで表される記号はすべて正の整数を表すものとします。
( 第 1 問 )
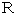 で割ったときに 1 余る数どうしを掛け合わせた数は、
で割ったときに 1 余る数どうしを掛け合わせた数は、 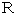 で割ると 1 余ることを証明せよ。
で割ると 1 余ることを証明せよ。-
2つの数を
 と
と  とし、 次のように置きます。
とし、 次のように置きます。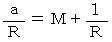
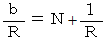
すると、
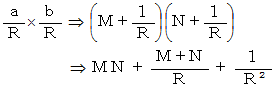
したがって、
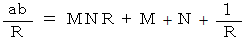
この式を見ると、
 と
と  を掛け合わせた数を
を掛け合わせた数を 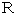 で割ると余りが 1 になることが解ります
で割ると余りが 1 になることが解ります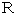 で割ったときに 1 余る数 と
で割ったときに 1 余る数 と 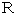 で割ったときに
で割ったときに 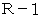 余る数を掛け合わせた数は、
余る数を掛け合わせた数は、 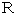 で割ると
で割ると 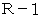 余ることを証明せよ。
余ることを証明せよ。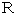 で割ったときに 1 余る数を
で割ったときに 1 余る数を  、
、 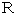 で割ったときに
で割ったときに 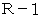 余る数を
余る数を  とし、 次のように置きます。
とし、 次のように置きます。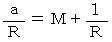
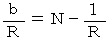
すると、
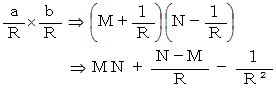
したがって、
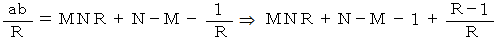
この式を見ると、
 と
と  を掛け合わせた数を
を掛け合わせた数を 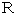 で割ると余りが
で割ると余りが 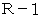 になることが解ります。
になることが解ります。-
1! = 1 → 1! を ( 1 + 1 ) で割ったときの余りは ( 1 + 1 ) − 1 です。
2! = 2 → 2! を ( 2 + 1 ) で割ったときの余りは ( 2 + 1 ) − 1 です。
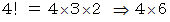
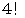 は、
は、 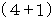 で割ったときの余りが 1 である数 と
で割ったときの余りが 1 である数 と 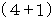 で割ったときの余りが
で割ったときの余りが 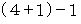 である数とが掛け合わされた数に等しいので、
である数とが掛け合わされた数に等しいので、 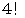 を
を 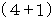 で割ったときの余りは
で割ったときの余りは 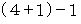 であることが解ります。
であることが解ります。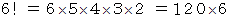
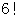 は、
は、 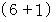 で割ったときの余りが 1 である数 と
で割ったときの余りが 1 である数 と 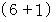 で割ったときの余りが
で割ったときの余りが 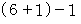 である数とが掛け合わされた数に等しいので、
である数とが掛け合わされた数に等しいので、 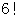 を
を 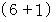 で割ったときの余りは
で割ったときの余りは 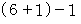 であることが解ります。
であることが解ります。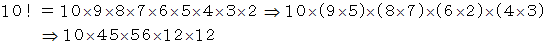
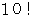 は、
は、 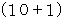 で割ったときの余りが 1 である数4つと
で割ったときの余りが 1 である数4つと 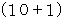 で割ったときの余りが
で割ったときの余りが 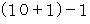 である数1つとが掛け合わされた数に等しいので、
である数1つとが掛け合わされた数に等しいので、 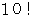 を
を 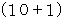 で割ったときの余りは
で割ったときの余りは 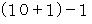 であることが解ります。
であることが解ります。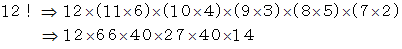
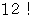 は、
は、 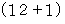 で割ったときの余りが 1 である数5つと
で割ったときの余りが 1 である数5つと 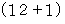 で割ったときの余りが
で割ったときの余りが 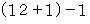 である数1つとが掛け合わされた数に等しいので、
である数1つとが掛け合わされた数に等しいので、 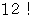 を
を 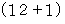 で割ったときの余りは
で割ったときの余りは 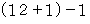 であることが解ります。
であることが解ります。以上のようにしてこの後もずっと見ていきますと、 興味深いことに、 素数から 1 を引いた数の階乗は、 その素数で割ると必ず余りがその素数から 1 を引いた数になることが解ります。 ウィルソンはこのことに気づき、 素数Pに関して次のような式が成り立っていることを発見しました。 ウィルソンの定理です。
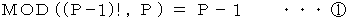
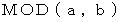 は
は  を
を  で割ったときの余りを表します。
で割ったときの余りを表します。式
 は、 次の式
は、 次の式  と同じです。
と同じです。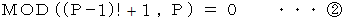
次の十進BASIC のプログラムは、 ウィルソンの定理を実際に確かめるものです。
次の十進BASIC のプログラムは、 ウィルソンの定理を利用して素数を探し出すものです。
 数理論 へ戻る
数理論 へ戻る