平方数の約数の個数は奇数で、 平方数以外の数の約数の個数は偶数。 　　なぜ？

　 素因数分解したときに　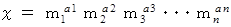　というふうに書ける
自然数 x の約数の個数は、 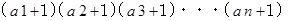　です。

　 x が平方数ならば、 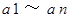はすべて偶数です。
したがって、 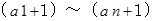はすべて奇数です。
したがって、 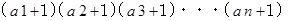は奇数です。

　 x が平方数でないならば、 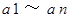のうち少なくとも１つは奇数です。
したがって、 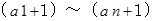のうち少なくとも１つは偶数です。
したがって、 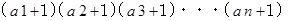は偶数です。

２ 〜 100 の自然数？　　　　

（ 問 題 ）

　 ロッカーが １ 番 〜 50番 まであります。 すべて扉は閉まっています。
エントリーナンバー １ 番 〜 50番 までの人がいます。
エントリーナンバー １ 番 から順に次のことをしてもらいます。
　 「 自分のエントリーナンバーの倍数の番号のロッカーだけを対象にして、
　 　扉が閉まっていれば開け、 開いていれば閉める。」
50人すべてがこの行為をし終わったとき、 扉の開いているロッカーの番号をすべて述べよ。

（ 解 答 ）

　 約数の個数が偶数か奇数かでロッカーの扉の開閉が決まります。
約数の個数が奇数ならロッカーの扉は開いています。
したがって、 答えは、 １、 ４、 ９、 16、 25、 36、 49　です。